Widerstand im Wechselstromkreis

Die Gesetze der Gleichstromtechnik gelten auch im Wechselstromkreis

Wirkwiderstand

Ohmsche Widerstände werden auch noch Wirkwiderstände genannt.

Spannung, Strom, Leistung

Wird ein ohmscher Widerstand \( R \) an eine sinusförmige Wechselspannung gelegt, so flieβt in ihm ein sinusförmiger Wechselstrom. Strom und Spannung liegen dabei in Phase, das heiβt beim Nulldurchgang der Spannungskurve hat auch die Stromkurve ihren Nulldurchgang.

$$u\left( t\right) =\hat{u} \cdot \sin \left( \omega t\right) $$ $$ i\left( t\right) =\hat{i} \cdot \sin \left( \omega t\right) $$

Herleitung Leistung

Die vom Widerstand aufgenommene Wirkleistung kann in jedem Augenblick durch berechnet werden.

$$ p\left( t\right) =u\left( t\right) \cdot i\left( t\right) =\hat{u} \cdot \hat{i} \cdot \sin^{2} \left( \omega t\right) $$ $$ mit\ \sin^{2} \left( \omega t\right) =\frac{1}{2} \cdot \left[ 1-\cos \left( 2\omega t\right) \right] $$

Siehe Collection des Formules Trigonométriques.

$$ p\left( t\right) =\frac{\hat{u} \cdot \hat{i} }{2} \left[ 1-\cos \left( 2\omega t\right) \right] =\frac{\hat{u} \cdot \hat{i} }{\sqrt{2} \cdot \sqrt{2} } \left[ 1-\cos \left( 2\omega t\right) \right] $$ $$ \Leftrightarrow p\left( t\right) =U\cdot I\cdot \left[ 1-\cos \left( 2\omega t\right) \right] $$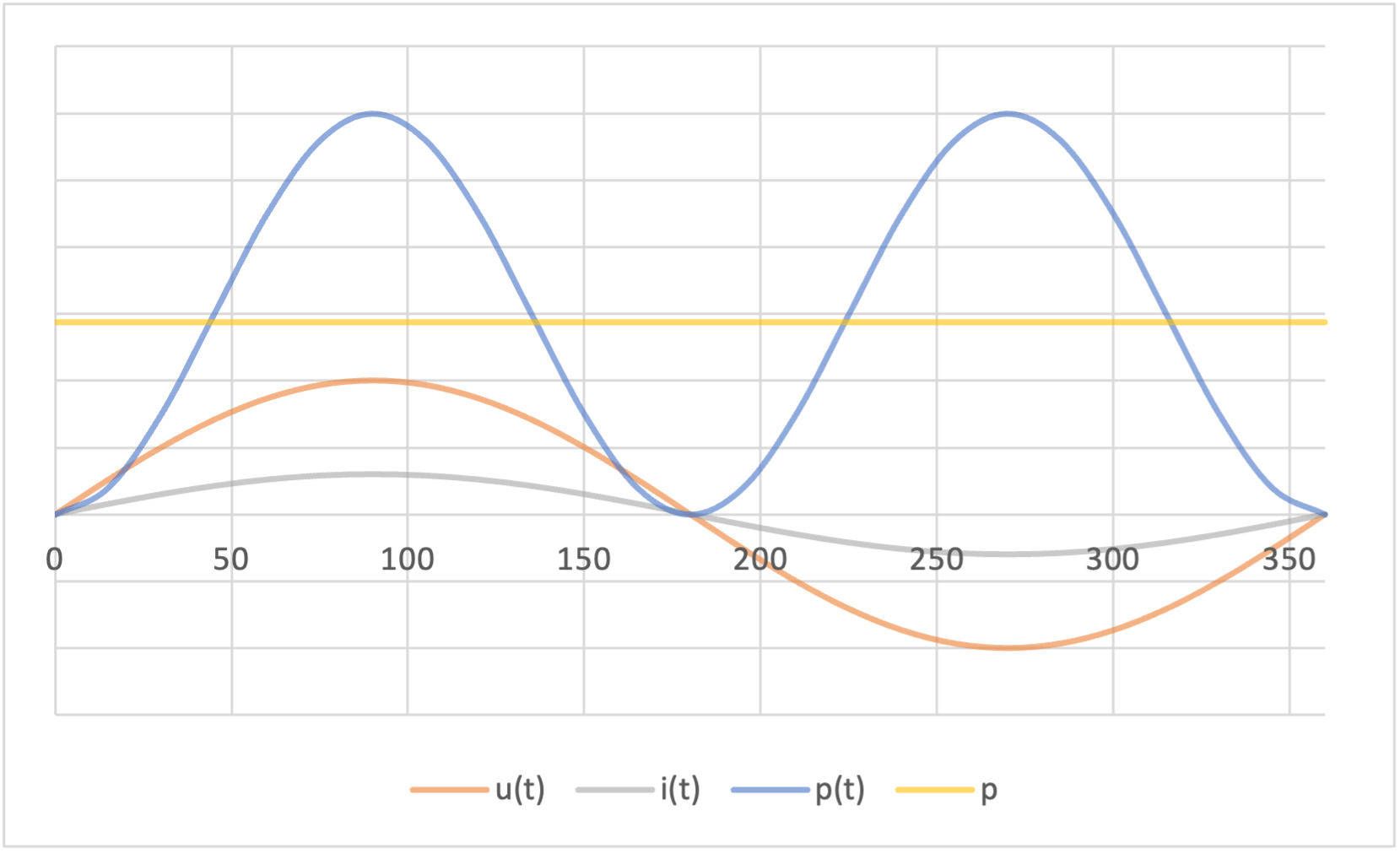

Wirkleistung

Die Leistung ist zu jedem Zeitpunkt positiv, das heiβt der Leistungsfluss verläuft stets vom Generator zum Widerstand. Die Leistungskurve stellt dabei eine Sinuskurve mit der doppelten Grundfrequenz dar.

Definition

Eine Wirkleistung ist eine Leistung, die zwischen \( p_{min}=0 \) und \( p_{min}= \hat{u} \cdot \hat{i} \) hin und her schwingt.