Kreisprozesse

Eine geschlossene Kurve im $ p $-$ V $-Diagramm bezeichnet man als Kreisprozess. Je nachdem in welchem Drehsinn die Kurve durchlaufen wird, unterscheidet man rechts- und linksgängige Kreisprozesse. Da bei dem Kreisprozess stets wieder der Anfangszustand erreicht wird, haben auch alle Zustandsgröβen nach einem Durchlauf des Kreisprozesses wieder ihre Ausgangswerte.

Rechtsgänginger Kreisprozess

Soll der Kreisprozess Arbeit nach auβen abgeben, so genannte Nutzarbeit, so muss die Kompressionskurve unterhalb der Expansionskurve verlaufen. Um das zu erreichen, muss vor oder während der Kompression gekühlt und vor oder während der Expansion geheizt werden. Dabei ergibt sich ein rechtsgängiger Durchlauf der Prozesskurve. Da derartige Maschinen Wärme in Arbeit oder Kraft umwandeln, nennt man sie Wärmekraftmaschinen.

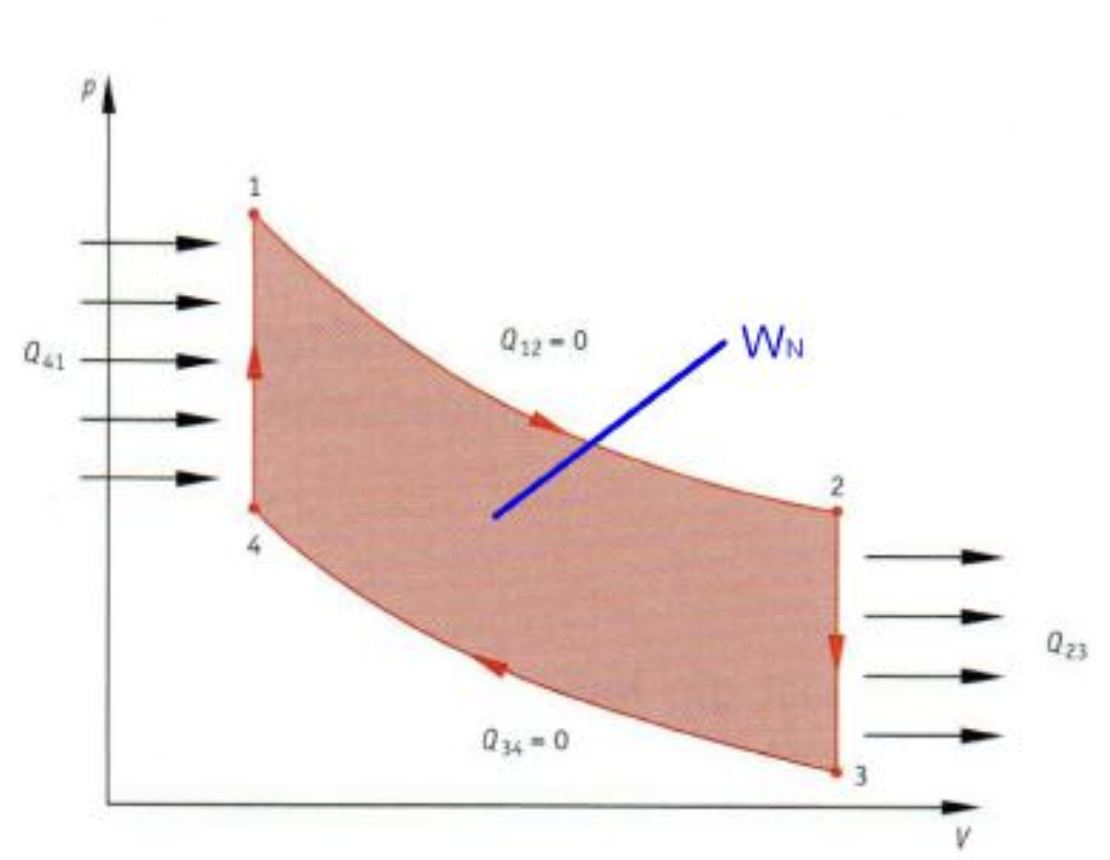
Daraus geht hervor, dass $ W_{12} $ die nach auβen abgegebene Expansionsarbeit ist, die betragsmäβig durch den Flächeninhalt unter der Expansionskurve repräsentiert wird. Das ist aber nicht die Nutzarbeit, die der Kreisprozess nach auβen abgibt, da von 3 nach 4 ein arbeitsaufnehmender Takt notwendig ist, dessen Betrag durch den Flächeninhalt unter der Kompressionskurve dargestellt wird. Man erkennt: Die Nutzarbeit kann durch Differenzbildung aus dem arbeitsliefernden Takt und dem arbeitsverzehrenden Takt bestimmt werden.Entsprechend findet man den Betrag der Nutzarbeit als Differenz der die Arbeitsbeträge darstellenden Flächeninhalte.

Nutzarbeit

Die Nutzarbeit $ W $ , die mit jedem Durchlauf des rechtsgängigen Kreisprozesses nach auβen abgegeben wird, entspricht betragsmäβig dem von der Kreisprozesskurve eingeschlossenen Flächeninhalt.

Energiebilanz

Für jeden Kreisprozess gilt:

$$ \sum Q+\sum W=0$$

mit $ W_{23}=W_{41}=0 $ und $ Q_{12}=Q_{34}=0 $ folgt:

$$Q_{12}+Q_{34}+W_{23}+W_{41}=0$$

mit $ W_{N}=W_{12}+W_{34} $

$$ W_{N}=W_{12}+W_{34}=-Q_{23}-Q_{41}$$ $$ |W_{N}|=|W_{12}|-W_{34}=Q_{41}-|Q_{23}|$$

Thermischer Wirkungsgrad

$$ \eta =\frac{Nutzen}{Aufwand} $$ $$ \eta =\frac{\left| W_{N}\right| }{Q_{zu}} =\frac{Q_{zu}-\left| Q_{ab}\right| }{Q_{zu}} =1-\frac{\left| Q_{ab}\right| }{Q_{zu}} $$

Linksgängige Kreisprozesse

Verläuft bei einem Kreisprozess die Kompressionskurve oberhalb der Expansionskurve, so wird dem Kreisprozess in der Bilanz Arbeit von auβen zugeführt. Bei solchen Prozessen wird die Prozesskurve im linksgängigen Drehsinn durchlaufen, weshalb man von linksgängigen Kreisprozessen spricht. Diese Kreisprozesse werden als Wärmepumpenprozesse bezeichnet.
Der Wärmepumpenprozess kann im Prinzip dadurch realisiert werden, dass man die Laufrichtung einer Wärmekraftmaschine umkehrt und ihr mechanische Arbeit zuführt. Diese aufgewandte Arbeit $ W_{auf}$, lässt sich auch beim Wärmepumpenprozess als Flächeninhalt der vom linksgängigen Kreisprozess eingeschlossenen Fläche wiederfinden.

Leistungszahl

Beim Wärmepumpenprozess, nur dieser wird im Folgenden betrachtet, ist die dem warmen Reservoir zugeführte Wärme der Nutzen. Damit ergibt sich die Leistungszahl zur Bewertung des Wärmepumpenprozesses wie folgt:

$$\varepsilon =\frac{Nutzen}{Aufwand} =\frac{\left| Q_{ab}\right| }{W_{auf}} =\frac{\left| Q_{ab}\right| }{\left| Q_{ab}\right| -Q_{zu}} =\frac{1}{\eta } $$

Die Leistungszahl des Wärmepumpenprozesses ist der Kehrwert des Wirkungsgrades beim Wärmekraftprozess. Für die Leistungszahl gilt offensichtlich stets: $ \varepsilon > 1 $.
Der Grenzfall $ \varepsilon = 1 $ hätte zur Folge, dass die Nutzwärme ausschlieβlich aus der aufgewandten Arbeit gespeist wird. Ein Wärmepumpen fände nicht mehr statt.

Carnot'sche Kreisprozess

Der Carnot'sche Kreisprozess stellt ein idealer Kreisprozess dar. Er besteht aus 2 Isothermen sowie 2 Adiabaten, wobei die Wärmeaufnahme und Wärmeabgabe bei konstanter Temperatur erfolgen.