Festigkeitslehre
Beanspruchung auf Zug
Im Werkstück entstehen Zugspannungen $\sigma_z$, welche senkrecht zum beanspruchten Querschnitt stehen. Solche Spannungen nennt man Normalspannungen.
Formel
$$ \sigma_z = \frac{F}{S} $$Beanspruchung auf Druck
Bei der Druckbeanspruchung entstehen mi Werkstück Druckspannungen $\sigma_{d}$ welche wie die Zugspannungen senkrecht zum beanspruchten Querschnitt stehen. Druckspannungen sind also auch Normalspannungen.
Formel
$$ \sigma_d = \frac{F}{S} $$Beanspruchung auf Abscherung
Hier entstehen mi Werkstück Scherspannungen $\tau_a$. Sie liegen inder Querschnittsfläche und man bezeichnet sie als Schubspannungen.
Formel
$$ \tau_a = \frac{F}{S} $$Beanspruchung auf Biegung
Bei der Biegebeanspruchung entstehen im Werkstück Normalspannungen welche als Zugspannungen oder Druckspannungen auftreten. In den Randfasern des Werkstücks sind die Spannungen am größten. Eine Faser ist spannungslos, man bezeichnet sie als neutrale Faser.
Formel
$$ \sigma_{bmax} = \frac{M_v}{l}$$Beanspruchung auf Verdrehung, Torsion
Die bei der Beanspruchung auf Verdrehung entstehenden Torsionsspannungen sind Schubspannungen. Die Randfasern werden am stärksten beansprucht während die Wellenachse spannungslos ist.
Formel
$$ \tau_{tmax} = \frac{M_tr}{l_p}$$Konvetion
$\sigma$ steht für Normalspannungen diese sind senkrecht zum Schnitt und $\tau$ (Tau) für Schubspannungen diese sind parallel zum Schnitt.
Zugspannungen
Der dargestellte Stab ist im Gleichgewicht unter Einwirkung der äuβeren Kräfte. Denken wir uns den Stab an einer beliebigen Stelle durchgeschnitten. Um das Gleichgewicht zu erhalten muss an der Schnittfläche die innere Kraft $F_N$ wirken. Da diese Kraft mit der äußeren Kraft $F$ mi Gleichgewicht ist muss sie senkrecht zur Schnittfläche stehen. Man bezeichnet sie deshalb als Normalkraft.
Die Kraft $F_N$ wirkt gleichmäßig auf alle Flächenteilchen des Querschnittes. Wir können ein Maβ für die Beanspruchung des Werkstoffes erhalten wenn wir die Kraft $F_N$ durch den Querschnitt teilen. Diese Gröβe nennt man Spannung. Da die verursachende Kraft eine Normalkraft ist erhalten wir eine Normalspannung. Die Zugspannung ist also eine Normalspannung da sie senkrecht zum beanspruchten Querschnitt steht.
Formeln
$$ Spannung = \frac{innere\ Kraft}{Querschnitt} $$ $$ \sigma_z = \frac{F_N}{S} $$da $F_N = F$:
$$ \sigma_z = \frac{F}{S} $$Einheiten
$$ [F] = N $$ $$ [S] = mm^2 $$ $$oder\ [S] = m^2 $$ $$[\sigma_z] = \frac{N}{mm^2}$$ $$oder\ [\sigma_z] = \frac{N}{m^2} = Pa$$Gefährdeter Querschnitt
Bei der Dimensionierung von Maschinenteilen müssen die Maβe so berechnet werden, dass eine bestimmte Spannung, die zulässige Spannung nicht überschritten wird.
|
Beschreibung |
Formel |
|---|---|
|
zulässige Zugspannung |
$\sigma_{z,\ zul} = \frac{F}{S}$ |
erforderlicher Querschnitt |
$S_{erf} = \frac{F}{\sigma_{z,\ zul}}$ |
vorhandene Spannung |
$\sigma_{z,\ vorha} = \frac{F}{S}$ |
|
maximale Belastung |
$F_{max} = S \cdot \sigma_{z,\ zul}$ |
Bei Berechnungen muss der Querschnitt der durch die Kraft $F$ belastet wird richtig erkannt werden. Es ist immer der kleinstmögliche Querschnitt.
Zugversuch
Beim Zugversuch wird ein zylindrischer Probestab einer langsam steigenden Belastung ausgesetzt. Der unbelastete Stab hat einen Querschnitt $S_0$ und eine Messstrecke $l_0$ ist durch zwei Markierungen auf dem Stab festgelegt.
Bezeichnen wir die Länge unter Belastung mit $l$ so beträgt die
Längenzunahme $\Delta l = l - l_0$.
Bezieht man die Längenzunahme auf die Messstrecke so erhält man die
Dehnung.
Formel
$$ Dehnung = \frac{Längenzunahme}{Meβstrecke} $$ $$\varepsilon = \frac{\Delta l}{l_0}$$Einheit
$$ [l] = mm^2$$ $$ [\varepsilon] \rightarrow keine\ Einheit$$Bemerkung
Die Dehnung $\varepsilon$ wird oft in % angegeben.
Durch den Zugversuch wird der Stab dünner. Wir erhalten also folgende gröβen:
$$ d_0,\ Stabdurchmesser\ ohne\ Belastung $$ $$ d,\ Stabdurchmesser\ unter\ Belastung $$ $$ \Delta d,\ Änderung\ des\ Stabdurchmesser $$Formel
$$ \varepsilon_q = \frac{\Delta d}{d_0} $$Bemerkung
Beide Gröβen werden normalerweise in $mm$ angegeben.
$$ [\varepsilon_q] \rightarrow keine\ Einheit$$Den Zusammenhang zwischen der Zugspannung $\sigma_z$ und der Dehnung $\varepsilon$ kann man in einem Diagramm darstellen : dem Spannungs Dehnungs Diagramm.
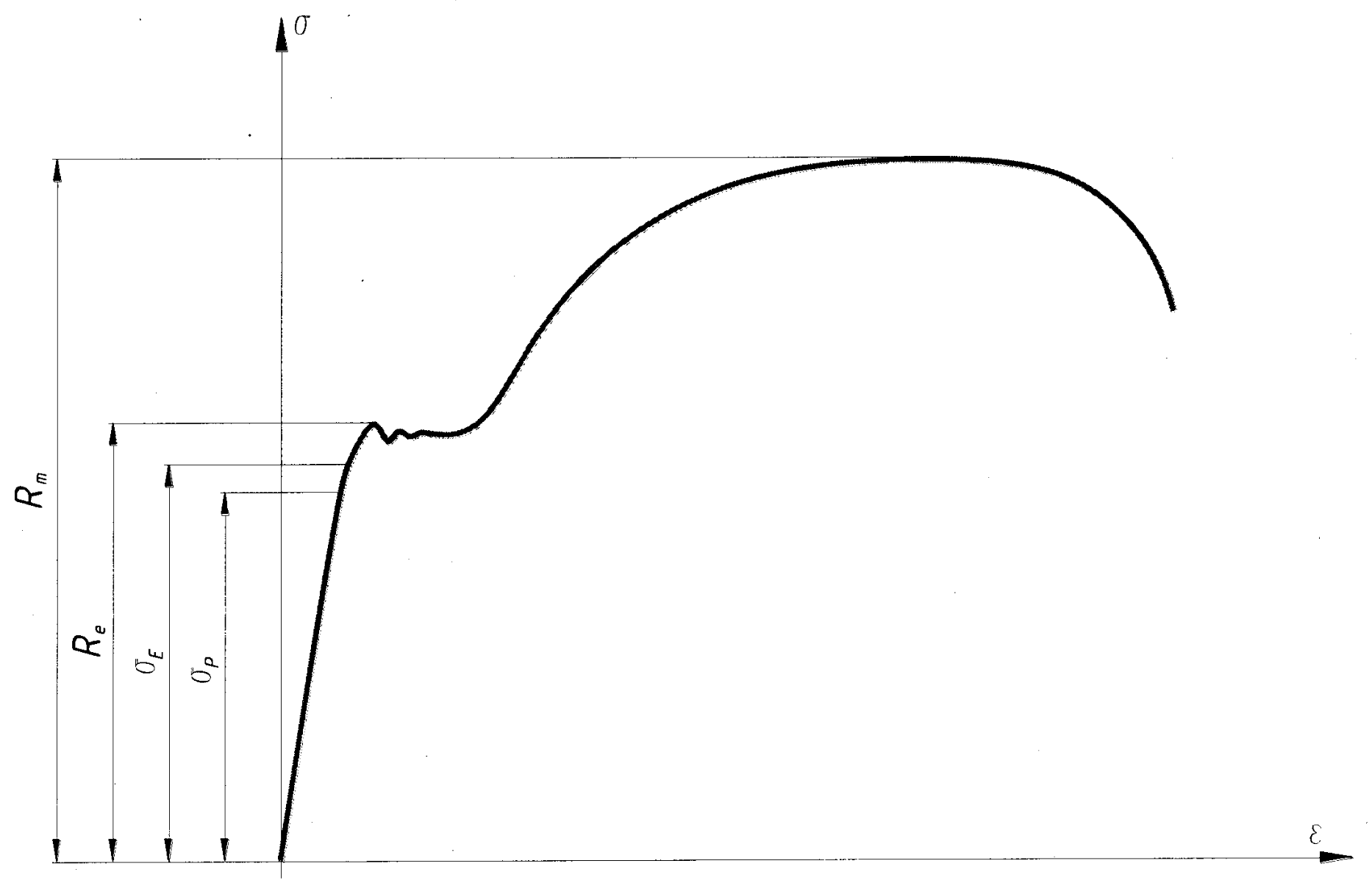
Wichtige Gröβen
-
Proportionalitätsgrenze $\sigma_P$
Bis zu dieser Grenze verlauft die Spannungs-Dehnungskurve linear. Die Spannung ist direkt proportional zur Dehnung.
-
Elastizitatsgrenze $\sigma_E$
Wird der Probestab nicht über die Spannung $\sigma_E$ hinaus beansprucht, so verhält sich der Stab elastisch, das heiβt nach Abklingen der Belastung ist keine bleibende Verformung zu erkennen.
-
Streckgrenze $R_e$
Ist die Streckgrenze erreicht, so beginnt der Werkstoff zu flieβen, das heiβt die Spannung fällt leicht ab und die Dehnung nimmt bei praktisch konstanter Spannung stark zu. Diese Streckgrenze ist nur bei weichen Stahlen ausgepragt, bei andern Werkstoffen ist sic nicht vorhanden.
-
Zugfestigkeit $R_m$
Nach dem Flieβen erholt sich der Werkstoff wieder und die Spannung steigt mit zunehmender Dehnung bis zu ihrem Höchstwert $R_m$. Danach nimmt die Spannung bei zunehmender Dehnung ab, bis der Bruch des Probestabes erfolgt. In diesem Bereich tritt eine starke Einschnürung auf.