Stehende Wellen
Reflexion von Transversalwellen
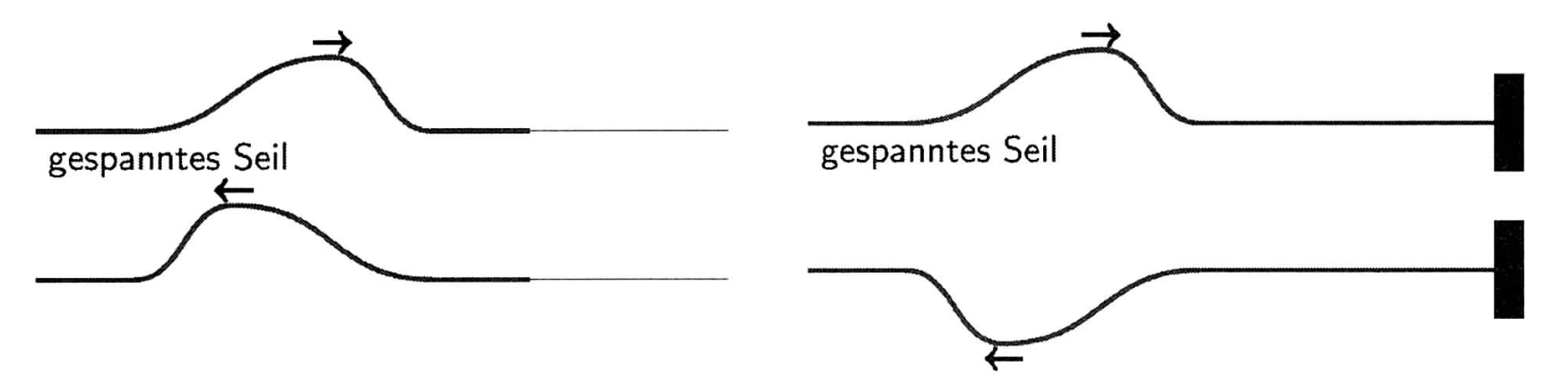
Eine Transversalwelle wird am freien Ende ohne Phasensprung, am festen Ende mit einem Phasensprung von $\pi$ reflektiert. Der Wellenberg kehrt am freien Ende als Wellenberg und am festen Ende als Wellental zurück.
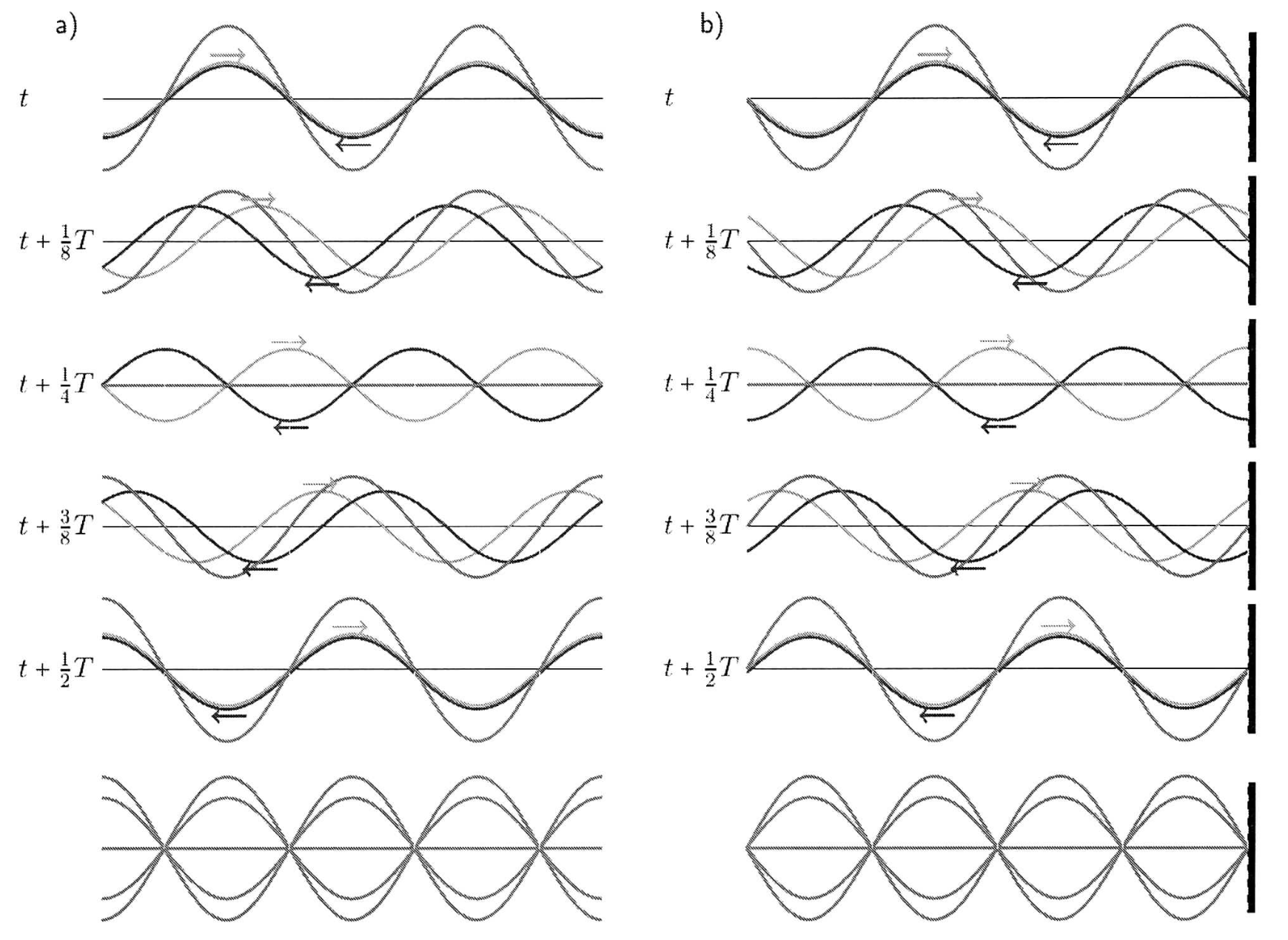
Entstehung von stehenden Wellen
Treffen zwei Wellen aufeinander welche eine Phasendifferenz von $\pi$
aufweisen, löschen sich diese bei der Überlagerung aus (destruktive
Interferenz), Dies geschieht an den Schwingungsknoten.
Treffen zwei Wellen aufeinander welche phasengleich sind, so verstärken
sie sich bei der Überlagerung (konstruktive Interferenz). Dies geschieht
an den Schwingungsbäuchen.
Eine stehende Welle entsteht durch Überlagerung zweier gegenläufiger
Wellen (die ankommende und die reflektierte) gleicher Frequenz und
gleicher Amplitude. In den Schwingungsbäuchen ist die Energie der Welle
gespeichert.
Eigenschwingungen
Am festen Ende eines Wellenträgers bildet sich ein Schwingungsknoten.
Am freien Ende eines Wellenträgers bildet sich ein Schwingungsbauch.
Der Abstand zwischen zwei Schwingungsknoten beträgt
$\frac{\lambda}{2}$.
frei-frei |
fest-frei |
fest-fest |
|---|---|---|
|
$n=0$ (Grundschwingung) 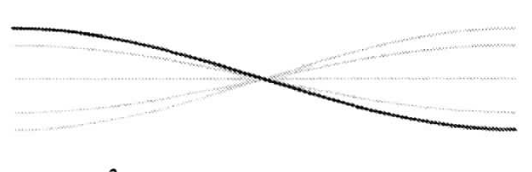
$L=\frac{\lambda_0}{2}$ und $f_0=f_0$ |
$n=0$ (Grundschwingung) 
$L=\frac{1}{2} \cdot \lambda_1$ und $f_0=f_0$ |
$n=0$ (Grundschwingung) 
$L=\frac{1}{2} \cdot \lambda_1$ und $f_0=f_0$ |
|
$n=1$ (1. Oberschwingung) 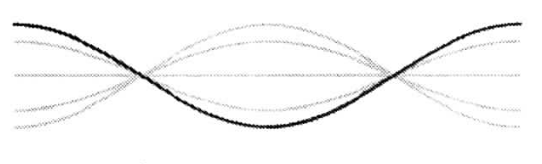
$L=2 \cdot \frac{\lambda_1}{2}$ und $f_1= 2 \cdot f_0$ |
$n=1$ (1. Oberschwingung) 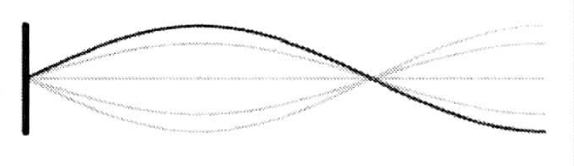
$L=\frac{3}{4} \cdot \lambda_1$ und $f_1=3 \cdot f_0$ |
$n=1$ (1. Oberschwingung) 
$L=\frac{2}{2} \cdot \lambda_1$ und $f_2= 1 \cdot f_0$ |
|
$n=2$ (2. Oberschwingung) 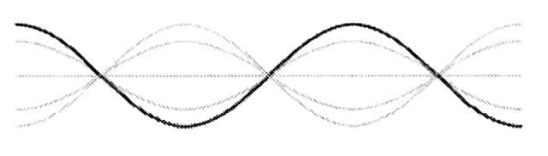
$L=3 \cdot \frac{\lambda_2}{2}$ und $f_2= 3 \cdot f_0$ |
$n=2$ (2. Oberschwingung) 
$L=\frac{5}{4} \cdot \lambda_1$ und $f_1=5 \cdot f_0$ |
$n=2$ (2. Oberschwingung) 
$L=\frac{3}{2} \cdot \lambda_1$ und $f_2= 3 \cdot f_0$ |
|
Verallgemeinerung: $$ L= \left( n+1 \right) \frac{\lambda_n}{2} $$ $$ \lambda_n = \frac{2L}{\left( n+1 \right)} $$ $$ \left( n \in \mathbb{N} \right) $$ |
Verallgemeinerung: $$ L= \left( 2n+1 \right) \frac{\lambda_n}{4} $$ $$ \lambda_n = \frac{4L}{\left( 2n+1 \right)} $$ $$ \left( n \in \mathbb{N} \right) $$ |
Verallgemeinerung: $$ L= \left( n+1 \right) \frac{\lambda_n}{2} $$ $$ \lambda_n = \frac{2L}{\left( n+1 \right)} $$ $$ \left( n \in \mathbb{N} \right) $$ |
Eigenfrequenzen eines Seils (fest-fest)
Mit dem Ausdruck für die Phasengeschwindigkeit einer Transversalwelle entlang eines Seils, welches an beiden Enden befestigt ist ergibt sich fur die Eigenfrequenzen eines elastischen Seils, welches an beiden Enden befestigt ist:
$$ f_n = \frac{n+1}{2L} \cdot \sqrt{\frac{F}{\mu}} $$mit: $n \in \mathbb{N}$
Eigenschwingungen
Es gilt:
Am geschlossenen Rohrende bildet sich ein Schwingungsknoten. Am offenen
Rohrende bildet sich ein Schwingungsbauch.
offen-offen |
offen-geschlossen |
|---|---|
|
$n=0$ (Grundschwingung) 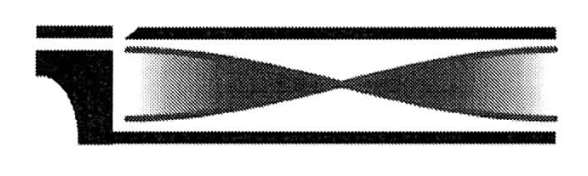
$L=\frac{\lambda_0}{2}$ und $f_0 = f_0$ |
$n=0$ (Grundschwingung) 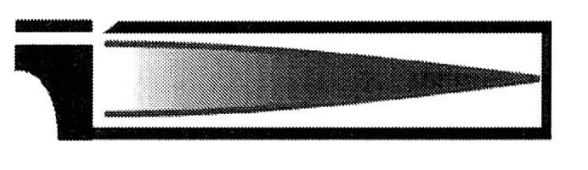
$L=\frac{1}{2} \cdot \lambda_1$ und $f_0 = f_0$ |
|
$n=1$ (1. Oberschwingung) 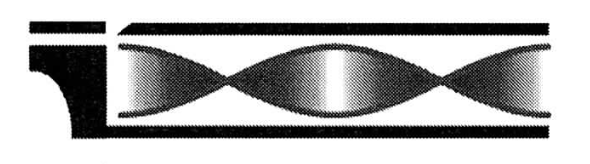
$L=2 \cdot \frac{\lambda_1}{2}$ und $f_1 = 2 \cdot f_0$ |
$n=1$ (1. Oberschwingung) 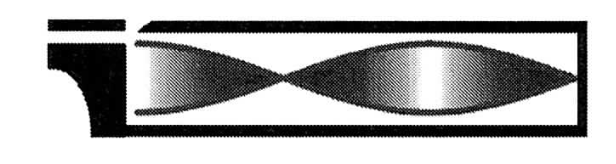
$L=\frac{3}{4} \cdot \lambda_1$ und $f_0 = 3 \cdot f_0$ |
|
$n=2$ (2. Oberschwingung) 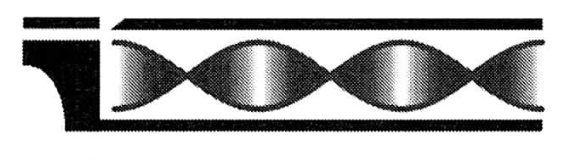
$L=3 \cdot \frac{\lambda_2}{2}$ und $f_2 = 3 \cdot f_0$ |
$n=2$ (2. Oberschwingung) 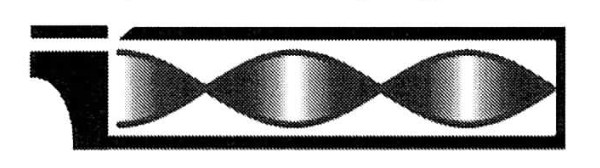
$L=\frac{5}{4} \cdot \lambda_2$ und $f_2 = 5 \cdot f_0$ |
|
Verallgemeinerung: $$ L = \left( n+1 \right) \frac{\lambda_n}{2} $$ $$ \lambda_n = \frac{2L}{\left( n+1 \right)} $$ $$ n \in \mathbb{N} $$ |
Verallgemeinerung: $$ L = \left( 2n+1 \right) \frac{\lambda_n}{4} $$ $$ \lambda_n = \frac{4L}{\left( 2n+1 \right)} $$ $$ n \in \mathbb{N} $$ |