Strahlenoptik

Reflektion

Es gibt 2 Arten von Reflektionen:

• Diffuse Reflektion

• Gesetzmäßige Reflektion

Reflektions Gesetz bei gemäßigter Reflektion

Der einfallende Strahl, das Lot und der reflektierte Strahl liegen in einer Ebene.
Der Einfallswinkel \( \alpha \) ist gleich dem Reflektionswinkel \( \alpha^{\prime} \)

$$ \alpha\ =\ \alpha^{\prime} $$

Das Lot

Das Lot (oder Einfallslot) ist eine Hilfslinie, welche senkrecht zum Spiegel steht, in dem Punkt wo der einfallende Lichtstrahl auf den Spiegel trifft.

Reelles, Virtuelles Bild

Reelles Bild

Wenn das Bild mittels eines Schirmes aufgefangen werden kann, dann ist das Bild reell.

Virtuelles Bild

Wenn das Bild nicht mittels eines Schirmes aufgefangen werden kann, dann ist das Bild virtuell.

Brechungsindex

Die Lichtgeschwindigkeit ist in materiellen Medien kleiner als im Vakuum.

Die Lichtgeschwindigkeit ist eine der wenigen exakten Naturkonstanten.

$$\approx 3\cdot 10^{8}\frac{m}{s} $$

Der Brechungsindex n oder Brechzahl eines Mediums ist definiert als der Quotient aus der Lichtgeschwindigkeit \( c_0 \) im Vakuum und der Lichtgeschwindigkeit \( c \) im Medium.

Definition

$$ n=\frac{Geschwindigkeit\ des\ Lichtes\ im\ Vakuum}{Geschwindigkeit\ des\ Lichtes\ im\ Medium} $$
$$ n=\frac{c_0}{c} $$

Zusammenhang zwischen den Brechzahlen und den Lichtgeschwindigkeiten

$$ \frac{n_{2}}{n_{1}} =\frac{\frac{c_{0}}{c_{2}} }{{}\frac{c_{0}}{c_{1}} } =\frac{c_{1}}{c_{2}} $$

Brechungsgesetz

$$ \frac{\sin \left( \alpha \right) }{\sin \left( \beta \right) } =konstant=\frac{n_{1}}{{}n_{2}} $$ $$ n_{1}\cdot \sin \left( \alpha \right) \ =\ n_{2}\cdot \sin \left( \beta \right) $$ $$ \alpha ,\ Winkel\ im\ Medium\ 1\ \left( Einfallswinkel\right) $$ $$\beta ,\ Winkel\ im\ Medium\ 2\ \left( Brechungswinkel\right) $$

Prinzip von Fermat

Das Licht nimmt den Weg der am wenigsten Zeit beansprucht.

Brechungsgesetzes von Snellius

Herleitung

Um von A nach B zu gelangen folgt der Strahl dem Prinzip von Fermat, er nimmt den Weg den die geringste Zeit beansprucht.

$$ t_{gesamt} = t_1 + t_2 = \frac{s_1}{c_1} + \frac{s_2}{s_2}$$

Um die minimale Zeit zu bestimmen berechnen wir die Ableitung und stellen diese gleich null.
Laut Pythagoras gilt im Rechtwinkeligen Dreieck:

$$ s_1 = \sqrt{x^{2}+y^{2}_{A}} $$ $$ s_2 = \sqrt{(x-x_B)^{2}+y^{2}_{A}} $$ $$ t^{\prime }_{gesamt}=\left( \frac{\sqrt{x^{2}+y^{2}_{A}} }{c_{1}} +\frac{\sqrt{\left( x-x_{B}\right)^{2} +y^{2}_{B}} }{c_{2}} \right)^{\prime} $$

Berechnung der Ableitungen

$$ A=\sqrt{x^{2}+y^{2}_{A}} \ \rightarrow \ A^{\prime }=\frac{x}{\sqrt{x^{2}+y^{2}_{A}} } $$ $$ B=\sqrt{\left( x-x_{B}\right)^{2} +y^{2}_{B}} \ \rightarrow \ B^{\prime }=\frac{-\left( x-x_{B}\right) }{\sqrt{\left( x-x_{B}\right)^{2} +y^{2}_{B}}} $$ $$ C=c_{1}\ \rightarrow \ C^{\prime }=0 $$ $$ D=c_{1}\ \rightarrow \ D^{\prime }=0 $$ $$ t^{\prime }_{gesamt}=\frac{x}{\sqrt{x^{2}+y^{2}_{A}} \cdot c_{1}} +\frac{-x+x_{B}}{\sqrt{\left( x-x_{B}\right)^{2} +y^{2}_{B}} \cdot c_{2}} $$ $$ =\frac{\sin \left( \alpha \right) }{c_{1}} -\frac{\sin \left( \beta \right) }{c_{2}} $$

Ein minimum liegt vor wenn die Ableitung gleich 0 ist.

$$ t^{\prime }_{gesamt}=\frac{\sin \left( \alpha \right) }{c_{1}} -\frac{\sin \left( \beta \right) }{c_{2}} =0$$ $$ \frac{\sin \left( \alpha \right) }{c_{1}} =\frac{\sin \left( \beta \right) }{c_{2}} $$ $$ \Longrightarrow \frac{\sin \left( \alpha \right) }{\sin \left( \beta \right) } =\frac{c_{1}}{c_{2}} =\frac{{}n_{2}}{n_{1}} $$

Daraus folgt das Brechungsgesetz von Snellius

$$\Longrightarrow n_{1}\cdot \sin \left( \alpha \right) =n_{2}\cdot \sin \left( \beta \right) $$

Totalreflektion

Bestimmung des Grenzwinkels

Mit dem Brechungsgesetz: \( \ n_{1}\cdot \sin \left( \alpha \right) =n_{2}\cdot \sin \left( \beta \right) \ \)
und \( \alpha =\alpha_{G} \ \left( in\ Medium\ 1 \right) \)
und \(\beta =90^{\circ }\ \left( in\ Medium\ 2\right) \)
Wir erhalten also aus dem Brechungsgesetz

$$\ n_{1}\cdot \sin \left( \alpha \right) =n_{2}\cdot \sin \left( \beta \right) \ $$ $$ n_{1}\cdot \sin \left( \alpha_{G} \right) =n_{2}\cdot 1 $$ $$ \sin \left( \alpha_{G} \right) =\frac{n_{2}}{n_{1}} $$ $$ \alpha_{G} =\arcsin \left( \frac{n_{2}}{n_{1}} \right) =\beta_{G} $$

Bemerkung

Da die Sinusfunktion auf -1 bis 1 definiert ist, gibt es keinen Winkel den der Lichtstrahl einnehmen könnte; deshalb erhalten wir das Phänomen : Totalreflektion.

Planparallele Platte

Fällt ein Lichtstrahl senkrecht auf eine planparallele Platte, so geht der Stahl ungebrochen hindurch. Fällt er schräg auf, so erfährt er beim Durchgang eine Parallelverschiebung.

Herleitung

Wir wollen einen Ausdruck für die Parallelverschiebung \( d \) mit \( h \) und \( \alpha \) und den Brechzahlen \( n_1 \) und \( n_2 \).
Im Dreieck \( ANC \) gilt:

$$ \cos \left( \beta \right) =\frac{AN}{AC} $$ $$ \Leftrightarrow AC=\frac{h}{\cos \left( \beta \right) } $$

Im Dreieck \( ABC \) gilt:

$$\sin \left( \alpha -\beta \right) =\frac{d}{AC} $$ $$ \Leftrightarrow AC=\frac{d}{\sin \left( \alpha -\beta \right) } $$

Suche nach einem Ausdruck für \( \beta \)
Brechungsgesetz:

$$ n_{1}\cdot \sin \left( \alpha \right) =n_{2}\cdot \sin \left( \beta \right) $$ $$ \Leftrightarrow \beta =\sin^{-1} \left[ \frac{n_{1}}{n_{2}} \cdot \sin \left( \alpha \right) \right] \ (1)$$ $$ AC = AC $$ $$ \Leftrightarrow \frac{h}{\cos \left( \beta \right) } =\frac{d}{\sin \left( \alpha -\beta \right) } \ (2) $$ $$ (2)\ in\ (1): $$ $$d=h\cdot \frac{\sin \left\{ \alpha -\sin^{-1} \left[ \frac{n_{1}}{n_{2}} \cdot \sin \left( \alpha \right) \right] \right\} }{\cos \left\{ \sin^{-1} \left[ \frac{n_{1}}{n_{2}} \cdot \sin \left( \alpha \right) \right] \right\} } $$

Prisma

Im Dreieck \( ABC \):
Die Summe der Internen Winkeln beträgt \( 180^{\circ } \):

$$ \left( 90^{\circ }-\beta_{1} \right) +\left( 90^{\circ }-\beta_{2} \right) +\gamma =180^{\circ }$$ $$ \Leftrightarrow 180^{\circ }-\beta_{1} -\beta_{2} +\gamma =180^{\circ }$$ $$ \Leftrightarrow -\beta_{1} -\beta_{2} +\gamma =0$$ $$\Leftrightarrow \gamma =\beta_{1} +\beta_{2} $$

Im Punkt \( C \):
Der platte Winkel beträgt \( 180^{\circ } \):

$$\left( 90^{\circ }-\alpha_{1} \right) +\gamma +\left( 90^{\circ }-\alpha_{2} \right) +\delta =180^{\circ }$$ $$\Leftrightarrow 180^{\circ }-\alpha_{1} +\gamma -\alpha_{2} +\delta =180^{\circ }$$ $$\Leftrightarrow -\alpha_{1} +\gamma -\alpha_{2} +\delta =0$$ $$\Leftrightarrow \delta =\alpha_{1} +\alpha_{2} -\gamma $$

Prismenwinkel, brechender Winkel

Definition

Der brechende Winkel \( \gamma \) ist der Winkel zwischen der Eintrittsfläche und der Austrittsfläche des Lichtstrahls.

Ablenkungswinkel, Gesamtablenkung

Definition

Der Ablenkungswinkel \( \delta \) ist der Winkel zwischen dem einfallenden und dem austretenden Lichtstrahl.

Minimalablenkung in einem Prisma

Formel der Ablenkung

$$ \delta =\alpha_{1} +\alpha_{2} -\gamma $$

Herleitung

Um die Minimalablenkung \( \delta_{min} \) zu bestimmen muss dei Ableitung einer Funktion in der \( \delta \) vorhanden ist aufgestellt werden, und die gleich Null stellen:

Berechnung des Brechungsgesetzes an der Eintrittsfläche

$$ n_{1}\cdot \sin \left( \alpha_{1} \right) =n_{2}\cdot \sin \left( \beta_{1} \right) $$ $$\Rightarrow \alpha_{1} =\sin^{-1} \left[ \frac{n_{2}}{n_{1}} \cdot \sin \left( \beta_{1} \right) \right] $$

Berechnung des Brechungsgesetzes an der Austrittsfläche

$$ n_{1}\cdot \sin \left( \alpha_{1} \right) =n_{2}\cdot \sin \left( \beta_{1} \right) $$ $$ \Rightarrow \alpha_{2} =\sin^{-1} \left[ \frac{n_{2}}{n_{1}} \cdot \sin \left( \beta_{2} \right) \right] $$ $$ mit\ \gamma =\beta_{1} +\beta_{2} $$ $$ \Rightarrow \alpha_{2} =\sin^{-1} \left[ \frac{n_{2}}{n_{1}} \cdot \sin \left( \gamma -\beta_{1} \right) \right] $$

Für die Ablenkung \( \delta \) gilt also:

$$ \delta =\sin^{-1} \left[ \frac{n_{2}}{{}n_{1}} \cdot \sin \left( \beta_{1} \right) \right] +\sin^{-1} \left[ \frac{n_{2}}{n_{1}} \cdot \sin \left( \gamma -\beta_{1} \right) \right] -\gamma $$

Für Minimalablenkung gilt:

$$ \frac{d\delta }{d\beta_{1} } =0$$ $$\Leftrightarrow \frac{\frac{n_{2}}{n_{1}} \cdot \cos \left( \beta_{1} \right) }{\sqrt{1-\left( \frac{n_{2}}{n_{1}} \right)^{2} \cdot \sin^{2} \left( \beta_{1} \right) } } +\frac{\frac{n_{2}}{n_{1}} \cdot \cos \left( \gamma -\beta_{1} \right) \cdot \left( -1\right) }{\sqrt{1-\left( \frac{n_{2}}{n_{1}} \right)^{2} \cdot \sin^{2} \left( \gamma -\beta_{1} \right) } } =0$$ $$ \Leftrightarrow \frac{\cos \left( \beta_{1} \right) }{\sqrt{1-\left( \frac{n_{2}}{n_{1}} \right)^{2} \cdot \sin^{2} \left( \beta_{1} \right) } } =\frac{\cos \left( \gamma -\beta_{1} \right) }{\sqrt{1-\left( \frac{n_{2}}{n_{1}} \right)^{2} \cdot \sin^{2} \left( \gamma -\beta_{1} \right) } } $$

Dies gilt nur wenn:

$$ \cos \left( \beta_{1} \right) =\cos \left( \gamma -\beta_{1} \right) $$ $$und$$ $$\sin^{2} \left( \beta_{1} \right) =\sin^{2} \left( \gamma -\beta_{1} \right)$$

Die Gleichungen sind nur wahr wenn:

$$\beta_{1} =\gamma -\beta_{1} $$

\( \delta \) ist minimal wenn:

$$ \beta_{1} =\frac{\gamma }{2} $$

Des weiteren gilt:

$$ \gamma =\beta_{1} +\beta_{2} $$ $$ \Rightarrow \beta_{2} =\frac{\gamma }{2} $$

Das heißt der Strahlengang verläuft symmetrisch durch das Prisma.

Fraunhoferformel

Herleitung

$$\delta_{min} =2\cdot \alpha_{1} -\gamma $$ $$ \Leftrightarrow \alpha_{1} =\frac{\delta_{min} +\gamma }{2} $$ $$und$$ $$ \gamma =\beta_{1} +\beta_{2}$$

Bei Minimalablenkung gilt:

$$ \Rightarrow \beta_{1} =\beta_{2} =\frac{\gamma }{2} $$

Setzt man diese Gleichungen in das Brechungsgesetz ein, so ergibt dies:

$$\sin (\alpha_{1} )=\sin \left( \frac{\gamma }{2} \right) $$ $$ \Leftrightarrow \sin \left( \frac{\delta_{min} +\gamma }{2} \right) =n\cdot \sin \left( \frac{\gamma }{2} \right) $$ $$ \Leftrightarrow n=\frac{\sin \left( \frac{\delta_{min} +\gamma }{2} \right) }{\sin \left( \frac{\gamma }{2} \right) } $$

Linsen

Eine Linse ist ein rotationssymmetrischer Körper der meist aus Glas oder Kunststoff hergestellt ist. Das optische Medium ist von zwei Kugelflächen begrenzt. Es ergeben sich zwei verschiedene Linsenarten.

Sammellinse, Konvexlinse

Es gibt:

1. Bikonvexlinsen

2. Plankonvexlinsen

3. Konkavkonvexlinsen

Skizzierung

Zerstreuungslinse, Konkavlinsen

Die Zerstreuungslinse, Konkavlinse ist in der Mitte dünner als am Rand.
Es gibt:

1. Bikonkavlinsen

2. Plankonkavlinsen

3. Konvexkonkavlinsen

Skizzierung

Hauptstrahlen bei Linsen

Brennpunkt

Ein Lichtbündel, welches parallel zur optischen Achse verläuft, wird nach dem Durchgang durch eine Sammellinse in einem Punkt gebündelt. Dieser Punkt wird Brennpunkt genannt.
Symmetrisch zum Mittelpunkt der Linse befindet sich der zweite Brennpunkt.

Brennweite

Die Distanz zwischen dem Mittelpunkt der Linse und dem Brennpunkt ist die Brennweite und wird mit dem Buchstaben \( f \) angeschrieben.

Sammellinse

Brennpunkte:
\( F_1 \) und \( F_2 \)
Brennweite:
\( OF_1\ =\ OF_2 =\ f \)

1. Ein Lichtstrahl, der parallel zur optischen Achse verläuft, verläuft nach der Brechung durch den Brennpunkt \( F_1 \). Ein Achsenparallelstrahl wird zum Brennpunktstrahl gebrochen.

2. Ein Lichtstrahl, der durch den Brennpunkt \( F_2 \) verläuft, verläuft nach der Brechung parallel zur optischen Achse weiter. Ein Brennpunktstrahl wird zum Achsenparallelstrahl gebrochen.

3. Ein Lichtstrahl, der durch den Mittelpunkt \( O \) verläuft, verläuft in gerader Linie weiter. Ein Mittelpunktstrahl wird nicht gebrochen.

Zerstreuungslinse

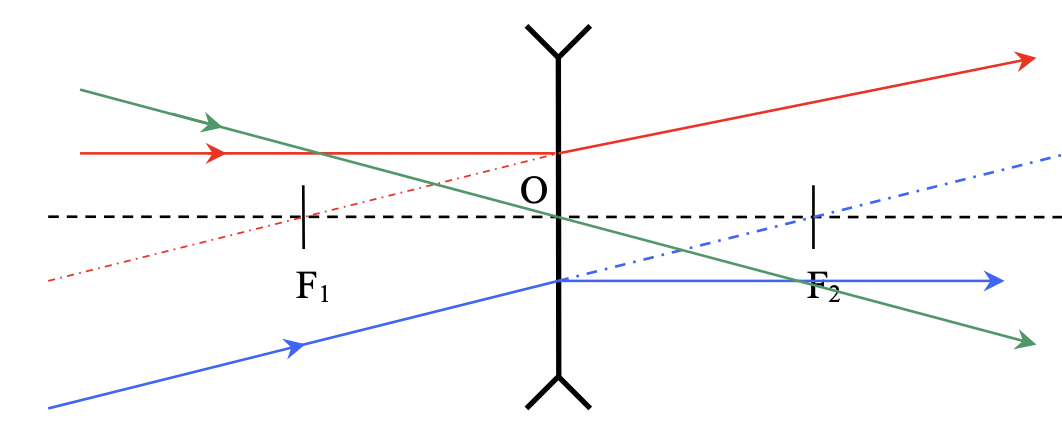
Brennpunkte:
\( F_1 \) und \( F_2 \)
Brennweite:
\( OF_1\ =\ OF_2 =\ f \)

1. Ein Lichtstrahl, der parallel zur optischen Achse verläuft, scheint nach der Brechung aus dem Brennpunkt \( F_1 \) zu kommen. Ein Achsenparallelstrahl wird zum Brennpunktstrahl gebrochen.

2. Ein Lichtstrahl, der durch den Brennpunkt \( F_2 \) verlaufen müsste, verläuft nach der Brechung parallel zur optischen Achse weiter. Ein Brennpunktstrahl wird zum Achsenparallelstrahl gebrochen.

3. Ein Lichtstrahl, der durch den Mittelpunkt \( O \) verläuft, verläuft in gerader Linie weiter. Ein Mittelpunktstrahl wird nicht gebrochen.

Bildentstehung an Linsen

1. reelle Bilder

   Die Strahlen konvergieren hinter der Linse, somit können diese Bilder auf einem Schirm aufgefangen werden.

2. virtuelle Bilder

   Die Strahlen divergieren hinter der Linse, somit können diese Bilder durch unser Auge erkannt werden, jedoch nicht auf einem Schirm sichtbar gemacht werden.

Ob reelle oder virtuelle Bilder entstehen, hängt von der Position des Gegenstandes zur Linse ab.

Es gilt:

$$F_1\ und F_2\, \ Brennpunkte$$ $$G,\ Gegenstandsgröße $$ $$B, \ Bildgröße $$ $$g, \ Gegenstandsweite$$ $$b, \ Bildweite $$ $$f,\ Brennweite$$

Bildkonstruktion Sammellinsen

Es gelten folgende Vorzeichenregeln:

1. Brennweite

   Sammellinse: \( f > 0 \)
   Zerstreuungslinse: \( f < 0 \)

2. Gegenstand

   reeller Gegenstand: \( g>0 \) und \( G>0 \)
   virtueller Gegenstand: \( g < 0 \) und \( G < 0 \)

3. Bild

   reeller Bild: \( b > 0 \) und \( B > 0 \)
   virtueller Bild: \( b < 0 \) und \( B < 0 \)

Bildkonstruktion Zerstreuungslinsen

1. Bild

   verkleinert; aufrecht, gerade; virtuell

Sehwinkel

Der Sehwinkel ist der Winkel unter dem ein Beobachter einen Gegenstand sieht. Er wird mit \( \omega \) bezeichnet.

Wir erhalten:

$$ \frac{G}{g} = \tan(\omega)$$

Bei kleinen Winkeln erhalten wir durch Kleinwinkelnäherung (wenn \( \omega \) in \( rad \) ):

$$ \omega = \frac{B}{b} = \frac{G}{g} $$

Einheit

Der Sehwinkel kann in \( rad \) oder in Sekunden \( s \) und Minuten \( min \) angegeben werden.

$$ 1^{\circ} = 60^{\prime}\ (min)$$ $$ 1^{\circ} = 3600^{\prime \prime}\ (s)$$

Abbildungsmaßstab

Herleitung

Da ähnliche Dreiecke:

$$ \tan(\omega) = \frac{G}{g} = \frac{B}{b} $$ $$ \Leftrightarrow \frac{B}{G} =\frac{b}{g} $$

Abbildungsmaßstab

$$ \Gamma = \left| \frac{B}{G} \right| $$

Der Abbildungsmaßstab gibt uns an, wie viel Mal das Bild größer als der Gegenstand ist und ist immer positiv.

Dioptrie

Oft wird nicht die Brennweite einer Linse angegeben, sondern ihre Brechkraft \( D \) in Dioptrien.

Formel

$$ D = \frac{1}{f} $$

Einheit

$$ \left[ D\right] =\frac{1}{m} =1dpt$$

Abbildungsgleichung

Herleitung

$$\tan \left( \alpha \right) =\frac{G}{g-f} =\frac{b}{f} $$ $$ \Leftrightarrow \frac{B}{G} =\frac{f}{g-f} =\frac{b}{g} $$ $$ \Leftrightarrow f\cdot g=b\left( g-f\right) $$ $$\Leftrightarrow f\cdot g=bg-bf$$ $$ \Leftrightarrow fg\ +bf=bg$$ $$\Leftrightarrow f\left( b+g\right) =bg$$ $$ \Leftrightarrow f=\frac{bg}{\left( b+g\right) } $$ $$\Leftrightarrow \frac{1}{f} =\frac{b}{bg} +\frac{g}{bg} \ $$ $$ \Leftrightarrow \frac{1}{f} =\frac{1}{g} +\frac{1}{b} \ $$