Probabilités

Dénombrement

Définition

Dénombrer, c'est calculer le nombre de possibilités de grouper un certain nombre d'éléments d'un ensemble.

Probabilité d'un événement

Définition

Soit une expérience aléatoire d'univers $\Omega$ fini, avec $\Omega = \{ e_1; e_2; ... ;e_n \}$

1. Définir une loi de probabilité sur $\Omega$, c'est associer à chaque issue $e_i$ un nombre positif $p(e_i)$ tel que:

   $$ p(e_1) + p(e_2) +...+ p(e_n) = 1 $$

2. Le nombre $p(e_i)$ est appelé : probabilité de l'événement élémentaire

3. La probabilité d'un événement $A$, notée $p(A)$, est la somme des probabilités de toutes les issues qui réalisent $A$.

Propriétés

1. La probabilité de l'événement certain $\Omega$ vaut:

   $$ p(\Omega) = 1 $$

2. La probabilité de l'événement impossible $\emptyset$ vaut:

   $$ p(\emptyset) = 0 $$

3. Pour tout événement $A$, on a:

   $$ 0 \leqslant p(A) \leqslant 1$$

4. Pour tout événement $A$, $p(A) + p(\bar{A}) = 1$

Définition

Si une expérience aléatoire d'univers $\Omega$, avec $\Omega = \{ e_1; e_2; ... ;e_n \}$. Si tous les événements élémentaires ont la même probabilité, on dit qu'ils sont équiprobable, et on a:

$$ p(e_1) = p(e_2) = ... = p(e_n) = \frac{1}{n} = \frac{1}{card \Omega } $$

Arrangement avec répétition

Arrangement avec répétition $B$ de $p$ éléments distincts ou non choisi parmi $n$ éléments distincts:

• Les $n$ éléments sont tous utilisés.

• Les éléments ne se répètent pas.

• Deux groupements diffèrent uniquement par l'ordre des éléments.

Formule

$$ B^{p}_{n}=n^{p} $$

Permutation

Permutation $P$ de $n$ éléments distincts:

• Les éléments donnés ne sont pas tous utilisés.

• Les $p$ éléments choisi peuvent se répéter.

• Deux groupements diffèrent soit par l'ordre soit par la nature des éléments.

  Formule

  $$P_{n}=n!$$

Arrangement sans répétition

Arrangement sans répétition $A$ de $p$ éléments distincts choisis parmi $n$ éléments distincts:

• Les $n$ éléments donnés ne sont pas tous utilisés.
• Les $p$ éléments choisis ne se répètent pas.
• Deux groupements diffèrent soit par l'ordre soit par la nature des éléments.

Formule

$$A^{p}_{n}=\frac{n!}{(n-p)!} $$ $$\left( p \leqslant n \right)$$

Combinaison

Combinaison $C$ de $p$ éléments distincts choisis parmi $n$ éléments distincts:

• Les $n$ éléments donnés ne sont pas tous utilisés.
• Les $p$ éléments choisis ne se répètent pas.
• Deux groupements diffèrent uniquement par la nature des éléments.

Formule

$$C^{p}_{n}=\frac{n!}{p!\left( n-p\right) !} =\frac{A^{p}_{n}}{P_{n}} $$ $$\left( p \leqslant n \right)$$

Vocabulaire des événements

Définition

1. Une expérience est dite aléatoire lorsqu'elle a plusieurs résultats possible et qu'on ne peut pas prévoir lequel sera obtenu. Le résultat d'une tell expérience est uniquement dû au hasard.

2. Une issue d'une expérience aléatoire est un résultat possible pour cette expérience.

3. L'ensemble de toutes les issues d'une expérience aléatoire est appelé univers associé à cette expérience.
   On note souvent: $\Omega$

4. Un événement $A$ est sous-ensemble de l'ensemble $\Omega$.
   On dit qu'une issue réalise un événement $A$ lorsque cette issue est un résultat appartenant à la partie $A$.

Schéma

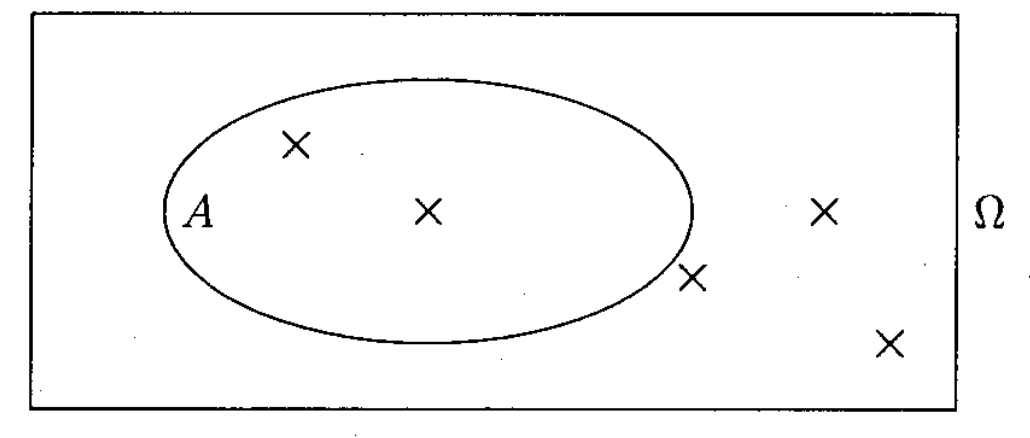
Événements particuliers

1. L'événement impossible est l'ensemble vide noté $\emptyset$ : aucune issue ne le réalise.

2. L'événement certain est l'univers $\Omega$: toutes les issues le réalisent.

3. Un événement élémentaire est un événement formé d'une seule issue.

Événements

Définition

L'intersection de $A$ et $B$, notée $A \bigcap B$ ou $A$ et $B$, est l'événement constitué des issues qui réalisent $A$ et $B$ en même temps.

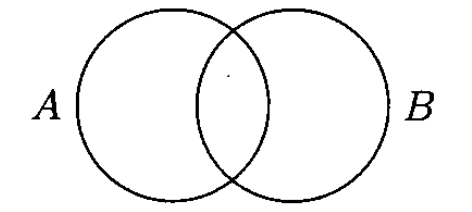
Définition

Dans le cas où $A$ et $B$ ne peuvent pas être réalisés en même temps, c'est à dire si $A \bigcap B \notin \emptyset$, on dit que $A$ et $B$ sont incompatible ou disjoint.

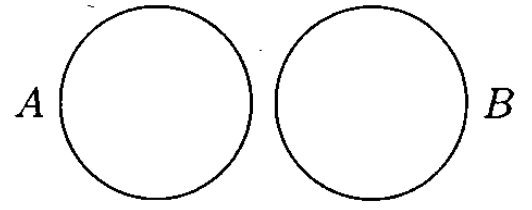
Définition

La réunion de $A$ et de $B$, notée $A \bigcup B$ ou $A$ ou $B$, est l'événement constitué des issues qui réalisent $A$ ou $B$, c'est à dire au moins l'un des deux.

Définition

L'événement contraire de $A$, noté $\bar{A}$ est constitué [...] de $\Omega$ qui ne réalisent pas $A$

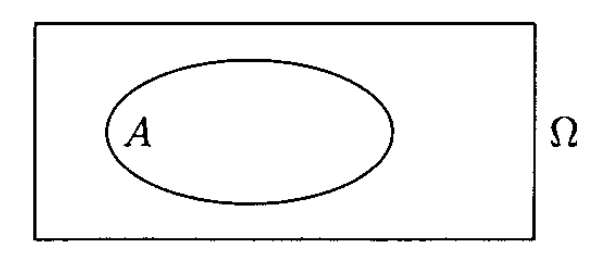
Propriété

Soit une expérience aléatoire où les événements élémentaires sont équiprobables et soit $A$ un événement, alors on a:

$$ p(A) = \frac{nombre\ d'issues\ de\ A}{nombre\ totales\ d'issues} $$ $$ =\frac{nombre\ d'issues\ favorable\ de\ A}{nombres\ d'issues\ possibles} $$

Arbres pondérés

Propriétés

• Dans un arbre pondéré, la probabilité d'un chemin est égale au produit des branches qui le composent.

• Dans un arbre pondéré, la probabilité d'un événement composé est égale à la sommes des probabilité qui le composent.

Variable aléatoire

Définition

Pour définir une variable aléatoire $X$ sur un univers $\Omega$ d'une expérience aléatoire, on associe un nombre réel $x_i$, a chaque éventualité $e_i$ de $\Omega$.

Probabilité d'une variable aléatoire

Définition

La loi de probabilité d'une variable aléatoire $X$ est la fonction qui à chaque valeur $x_i$ prise par $X$ associe la probabilité: $p \left( X = x_i \right)$

Espace mathématiques

Definition

L'espérance mathématique de la variable aléatoire $X$, notée $E \left( X \right)$ est la somme des produits de chaque valeur prise par $X$ par la probabilité que $X$ prenne cette valeur :

$$ E \left( X \right) = \sum^{k}_{i=1} x_{i}\cdot P\left( X=x_{i}\right) $$ $$ = x_1 \cdot p \left( X = x_1 \right) + x_2 \cdot p \left( X = x_2 \right) + ... + x_k \cdot p \left( X = x_k \right) $$

Propriété

Si $X$ est une variable aléatoire égale au gain algébrique d'un jeu hasard, alors $ E \left( X \right)$ représente le gain moyen auquel on peut s'attendre.

• Si $ E \left( X \right) > 0$, on dit que le jeu est favorable au joueur.

• Si $ E \left( X \right) = 0$, on dit que le jeu est équitable au joueur.

• Si $ E \left( X \right) < 0$, on dit que le jeu est défavorable au joueur.

Variance

Définition

On appelle variance d'une variable aléatoire $X$ le nombre $V(X)$ défini par:

$$ V \left( X \right) = \sum^{k}_{i=1} \left( x_{i}-E\left( X\right) \right)^{2} \cdot p\left( X=x_{i}\right) $$ $$ = \left( x_{1}-E\left( X\right) \right)^{2} \cdot p\left( X=x_{1}\right) + \left( x_{2}-E\left( X\right) \right)^{2} \cdot p\left( X=x_{2}\right) +... +\left( x_{k}-E\left( X\right) \right)^{2} \cdot p\left( X=x_{k}\right) $$

Propriété

$$ V \left( X \right) = \sum^{k}_{i=1} x^2_i \cdot p\left( X=x_{i}\right) - \left( E \left( X \right) \right)^2 $$ $$ = x^{2}_{1}\cdot p\left( X=x_{1}\right) + x^{2}_{2}\cdot p\left( X=x_{2}\right) + ... + x^{2}_{k}\cdot p\left( X=x_{k}\right) - \left( E \left( X \right) \right)^2 $$ $$ = E \left( X^2 \right) - \left( E \left( X \right) \right)^2$$

Écart type

Definition

On appelle écart type d'une variable aléatoire $X$ le nombre $\sigma(X)$ défini par:

$$ \sigma(X) = \sqrt{V(X)} $$

Propriété

Plus l'écart type et la variance sont grands, plus la variable aléatoire est dispersée.