Systems of Linear Equations

System of equations

A system of equations is a collection of finitely many equations involving the same set of variables.
The system may not contain any functions or variables with a degree higher then 1.

Solution of the system

• The solution of the system is the intersection of the solution sets of each equation.

• If some equation has no solution, the system has no solution.

• It is possible that each equation has a solution but not the system.

Lines

A line in $\mathbb{R}^{2}$: take $a,b,c \in \mathbb{R}$ with $a,b \neq 0$, we obtain for the equation of a line:

$$ ax + by = c $$

$a,b,c$ are constants and $x,y$ are variables.

Planes

Plane in $\mathbb{R}^{3}$: take $a,b,c,d \in \mathbb{R}$ with $a,b,c \neq 0$, we obtain for the equation of a plane:

$$ ax + by + cz = d $$

$a,b,c,d$ are constants and $x,y,z$ are variables.

Linear equations

A linear equation has $n$ variables $x_1, ..., x_n$:

$$ a_1 x_1 + a_2 x_2 + ... + a_n x_n = b$$

$a_1,a_2, ... ,a_n, b$ are constants and $x_1,x_2, ... ,x_n \neq 0$ .

Constant term

The term that doesn't have a variable associated with that term is called a constant term.

Homogeneous linear equation, Homogeneity

If a systems constant term is zero it is refered to as a homogeneous linear equation.

Remark

If the system represents a line, the line passes through the origin of the coordinate system.

Linear system, System of linear equations

A linear system or a system of linear equations with the variables $x_1, ..., x_n$ where $n \in \mathbb{N}$ is:

$$\begin{align*} \left\{ \begin{array}{ccccccccccc} a_{1,1}x_{1} & + & a_{1,2}x_{2} & + & \cdots & + & a_{1,n}x_{n} & = & b_{1} \\ a_{2,1}x_{1} & + & a_{2,2}x_{2} & + & \cdots & + & a_{2,n}x_{n} & = & b_{2} \\ \vdots & & \vdots & & \ddots & & \vdots & & \vdots \\ a_{m,1}x_{1} & + & a_{m,2}x_{2} & + & \cdots & + & a_{m,n}x_{n} & = & b_{m} \\ \end{array} \right. \end{align*} $$

With $a_{ij}$ for $i=1,...,m$ and $j=1,...,n$ and $b_k$ for $k=1,...,m$ are constants.

Solution of a linear system

A solution of the linear system with the variables $x_1, . . . , x_n$ is a sequence of numbers $(s_1, . . . , s_n)$ such that the substitution makes the following equation a true equality:

$$ x_1 = s_1;\ x_2 = s_2;\ ... x_n = s_n $$

Remark

The solution is an ordered pair, an ordered triple, or in general an ordered $n$-tuple.

Tuple

Definition

A tuple is a finite sequence or ordered list of numbers or, mathematical objects, which are called the elements of the tuple.

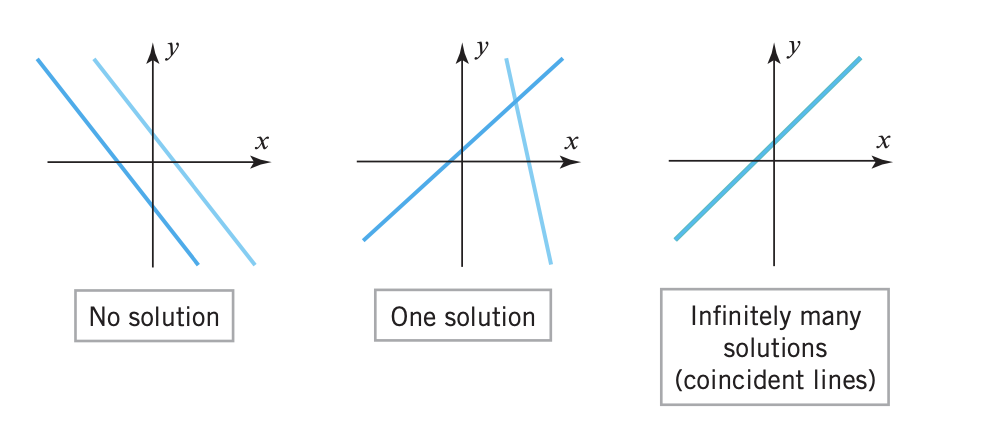
Solution sets for lines

For a linear system with $a,b \neq 0$ as variables the equation represents a line in the real plane $\mathbb{R}^2$. We therefore get 3 possible scenarios:

• The lines are parallel and distinct: no solution

  $$ L_1 \| L_2 $$

• The lines intersect: exactly one exact solution

  $$ L_1 \cap L_2 $$

• The lines coincide: infinitely many solutions

  $$ L_1 = L_2 $$

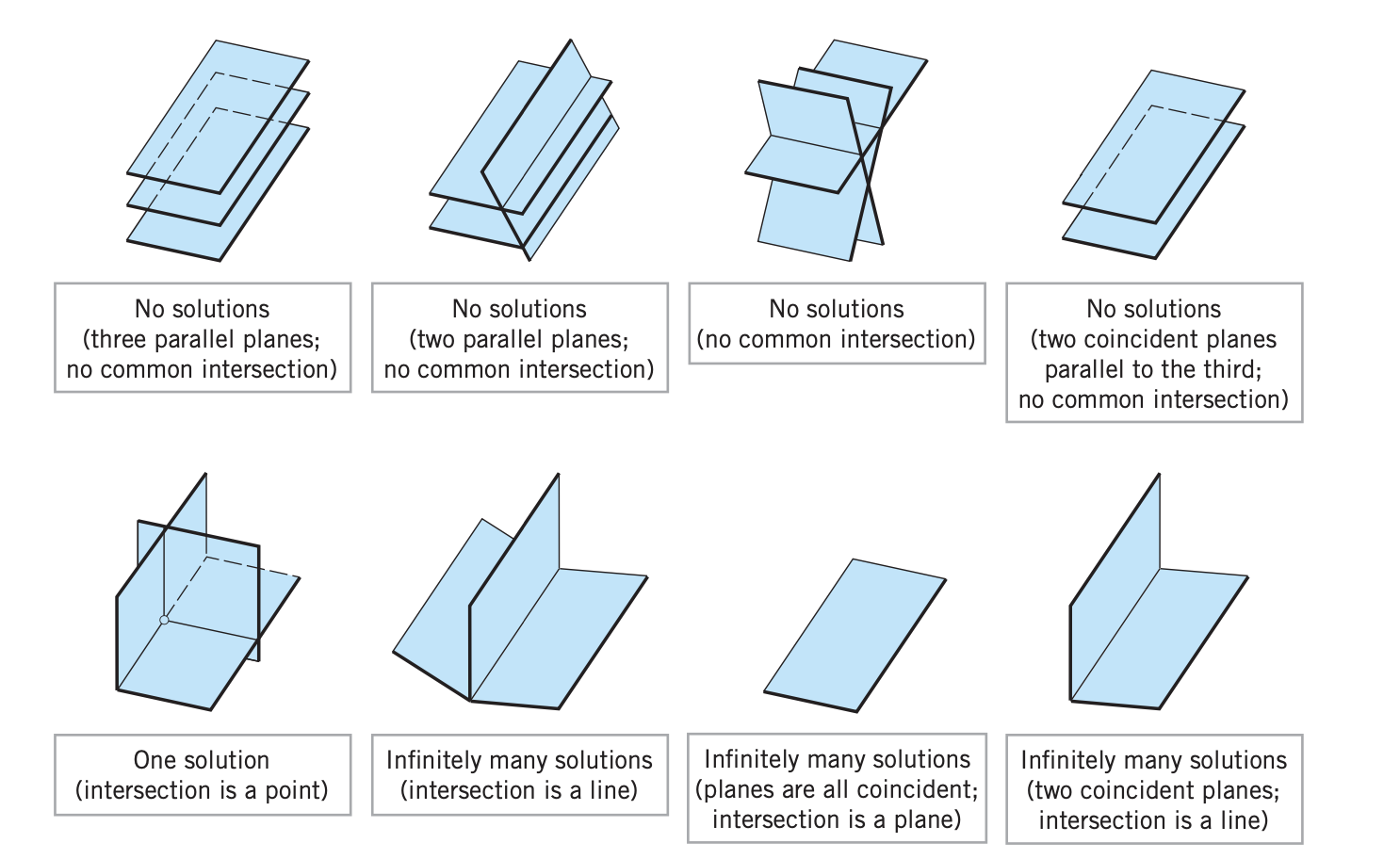
Solution sets for planes

For a linear system with $a,b,c \neq 0$ as variables the equation represents a plane in real space $\mathbb{R}^3$. We therefore get 8 possible scenarios:

• The planes are parallel: no solution

  $$ P_1 \| P_2 \| P_3 $$

• One plane intersects 2 parallel planes: no solution

  $$ P_1 \cap \left( P_2 \| P_3 \right)$$

• The planes intersect each other but at no common line $L_s$: no solution

  $$ P_1 \cap P_2 \cap P_3 \neq L_s $$

• One plane coincides one other plane and a third is parallel to the them: no solution

  $$ P_1 \| \left( P_2 = P_3 \right)$$

• All 3 planes are at angles $\theta , \alpha \neq 0$ to each other and the angle follows no plane, the solution is a point $S_p$: one exact solution

  $$ P_1 \cap P_2 \cap P_3 = S_p$$

• All 3 planes are at angles $\theta , \alpha \neq 0$ to each other and the angle follows one plane, the solution is a line $L_s$: infinitely many solutions

  $$ L_s = P_1 \cap P_2 \cap P_3 $$

• The planes are all coincide, the solution is the entire plane: infinitely many solutions

  $$ P_1 = P_2 = P_3 $$

• Two planes coincide and one of them is at an angle $\theta \neq 0$ to the planes, the solution is a line: infinitely many solutions

  $$ (P_1 = P_2) \cap P_3 $$

Remark

Every linear system has either zero, one or infinitely many solutions.

Infinitely many solutions

If a solution to a linear equation has infinitely many solutions, the solution is expressed with finitely many parameters to which we can assign arbitrary values in $\mathbb{R}$.

Remark

The parameter is commonly called $t$.

Consistent

A linear equation is consistent if it has at least one solution, the solution set is not empty.

Remark

A homogeneous system is always consistent. It has at least one trivial solution, where all variables are 0.

Inconsistent

A linear equation is inconsistent if it has at no solution, the solution set is empty.

Augmented matrix

Definition

The augmented matrix is the matrix that is formed by appending the column of constant terms to the end of the matrix formed by the coefficients.

Constructing an augmented matrix

For the following generalised linear equation:

$$\begin{align*} \left\{ \begin{array}{ccccccccccc} a_{1,1}x_{1} & + & a_{1,2}x_{2} & + & \cdots & + & a_{1,n}x_{n} & = & b_{1} \\ a_{2,1}x_{1} & + & a_{2,2}x_{2} & + & \cdots & + & a_{2,n}x_{n} & = & b_{2} \\ \vdots & & \vdots & & \ddots & & \vdots & & \vdots \\ a_{m,1}x_{1} & + & a_{m,2}x_{2} & + & \cdots & + & a_{m,n}x_{n} & = & b_{m} \\ \end{array} \right. \end{align*} $$

• We associate a row to each equation

• We associate a column to each variable, in a preserved order for each equation

• We also consider one additional column to take care of the constant term

After these steps we obtain:

$$ \begin{bmatrix}a_{1,1}&a_{1,2}& \cdots &a_{1,n}&b_{1}\\ a_{2,1}&a_{2,2}& \cdots &a_{2,n}&b_{2}\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ a_{m,1}&a_{m,2}& \cdots &a_{m,n}&b_{m}\end{bmatrix} $$

Elementary row operations

Elementary row operations are:

• Multiply a row through by a non zero constant

• Interchange two rows

• Add a constant times one row to another

Definition

Elementary row operations are the most basic operations done to solve the system.

Row echelon form

For a matrix to be in row echelon form, it needs to satisfy all of the following conditions:

• If there are any rows that consist entirely of zeros, then they are grouped together at the bottom of the matrix

• If a row does not consist entirely of zeros, then the first nonzero number in the row is a 1. We call this a leading 1

• In any two successive rows that do not consist entirely of zeros, the leading 1 in the lower row occurs farther to the right than the leading 1 in the higher row

Reduced row echelon form

For a matrix to be in reduced row echelon form, it needs to satisfy all of the conditions to be in row echelon form as well as:

• Each column that contains a leading 1 has zeros everywhere else in that column

Gaussian elimination

The Gaussian elimination is the standard procedure to turn a matrix into row echelon form.

Gaussian elimination procedure

We start with the left most nonzero column $C$:

• Swap rows so that the top entry of $C$ is non zero. For this swap we use the first suitable row.

• Multiply the top row by a non-zero constant and make the top entry of $C$ a 1.

• Add suitable multiples of the top row to the other rows and make sure that all entries of $C$ apart from the top one are 0.

After this the first row is now completed and we continue to iterate through the remaining submatrix.
This process goes on until the all the rows are covered or until all remaining rows consist of zeros.

Gauss-Jordan elimination

The Gauss-Jordan elimination is the standard procedure to turn a matrix into reduced row echelon form.

Gauss-Jordan elimination procedure

We start with the last nonzero row $R$:

• Consider the leading 1 of $R$ which is in some column $C$

• Multiply $R$ by non-zero constants and add it to previous rows and make 0 all other entries of $C$ apart from the leading 1.

After this the first row is now completed and we continue to iterate through the remaining submatrix.
This process continues until all entries above all leading 1's are zero.

Associated homogeneous linear system

Every inhomogeneous linear system has an associated homogeneous linear system, where the constant terms are zero.

Superposition principle

For a consistent inhomogeneous linear system:
All solutions are obtained by summing to the chosen solution, the solutions of the associated homogeneous linear system.

Proof

Consider the linear system where the i ^th equation is:

$$ \sum_{h=1}^{n} a_{ih}x_{h}=b_{i} $$

The corresponding homogeneous linear system is:

$$ \sum_{h=1}^{n} a_{ih}x_{h}=0 $$

Let $(X_1, . . . , X_n)$ be a fixed solution, $(x_1, . . . , x_n)$ any solution, $(y_1, . . . , y_n)$ any solution of the homogeneous system. Then:

$$ \sum_{h=1}^{n} a_{ih}\left( x_{h}-X_{h} \right) =\sum_{h=1}^{n} a_{ih}x_{h}-\sum_{h=1}^{n} a_{ih}X_{h} $$ $$ =b_{i}-b_{i} $$ $$ =0 $$

so $(x_1−X_1, . . . , x_n−X_n)$ is a solution of the homogeneous system. Conversely,

$$ \sum_{h=1}^{n} a_{ih}\left( x_{h}+X_{h} \right) =\sum_{h=1}^{n} a_{ih}x_{h}+\sum_{h=1}^{n} a_{ih}X_{h} $$ $$ =b_{i}+b_{i} $$ $$ =0 $$

so summing to $(X_1, . . . , X_n)$ any solution of the homogeneous system gives again a solution.

$\square$

Number of parameters in the solution

For nonzero solution set, any consistent linear system:
The number of parameters in the solution set is the number of free variables.

Number of free variables

The number of free variables is the number of variables minus the number of leading variables.

Number of leading variables

The number of leading variables is the number of non-zero rows in the row echelon form.