Schaltnetze

Serielle Gatterschaltung, UND-Verknüpfung

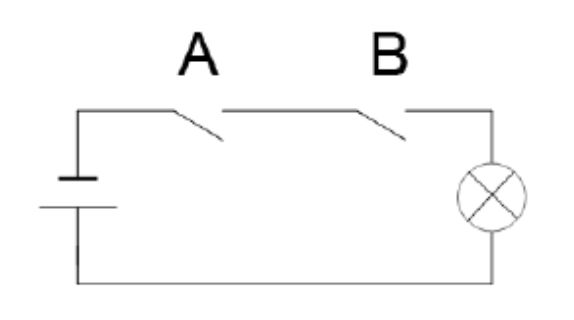
Die serielle Schaltung realisiert die logische Konjunktion: \( Y = A \land B \). Der Stromkreis ist nur geschlossen, wenn beide Schalter A und B aktiviert sind. Diese Grundform findet sich in Sicherheitsschaltungen, wo zwei unabhängige Bestätigungen benötigt werden.

Parallele Gatterschaltung, ODER-Verknüpfung

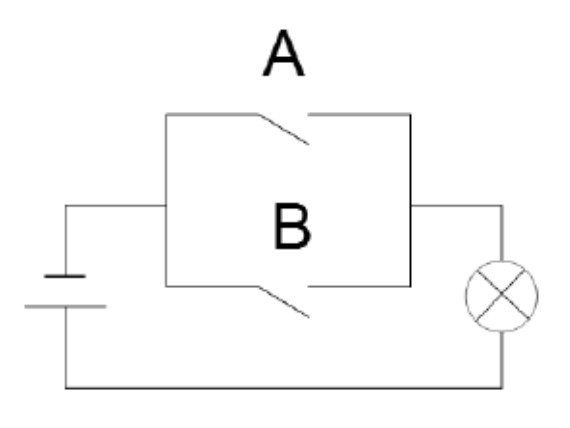
Die parallele Schaltung realisiert die logische Disjunktion: \( Y = A \lor B \). Hier reicht die Aktivierung eines beliebigen Schalters aus, um den Stromkreis zu schließen.

Physikalische Realisierung der Transistoren

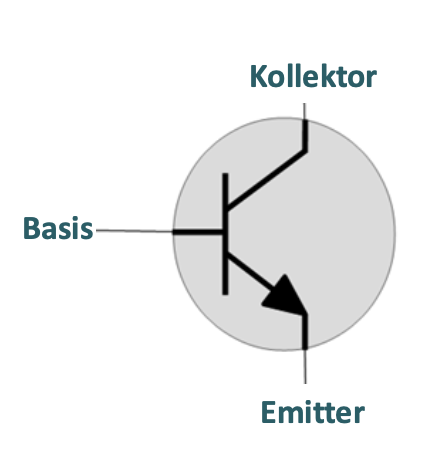
Transistoren sind die fundamentalen Bauelemente der Digitaltechnik. Als Halbleiterbauelemente können sie durch Anlegen einer Steuerspannung zwischen Basis und Emitter den Stromfluss zwischen Kollektor und Emitter schalten.

Funktionsweise von Transistoren

Bei einem NPN-Transistor fließt ein Basisstrom, der einen größeren Kollektorstrom ermöglicht. Diese Stromverstärkung ermöglicht die Kaskadierung von Logikgattern. Die Miniaturisierung führte zu integrierten Schaltkreisen, ICs genannt, mit milliardenfacher Transistordichte.

Mehr über Transistoren ist hier zu finden.

Inverter, NOT-Gatter

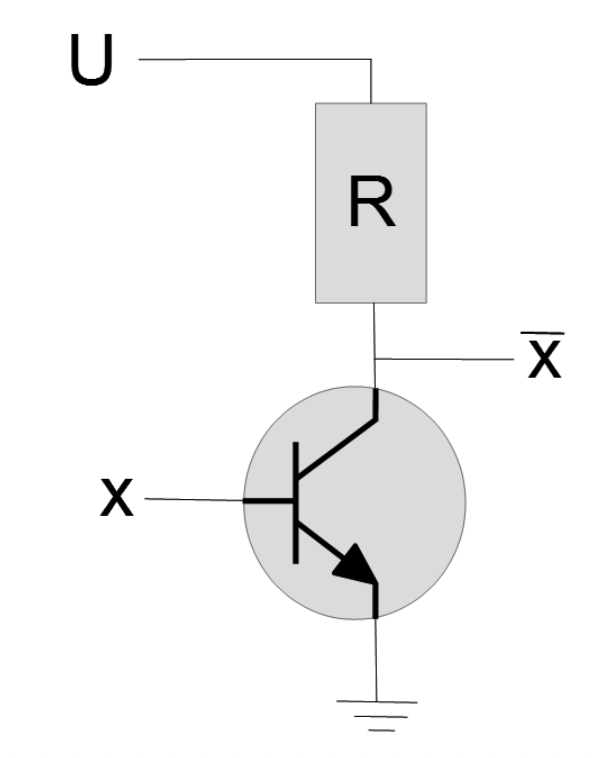
Realisiert die Negation: \( Y = \overline{A} \). Ein High-Pegel am Eingang schaltet den Transistor durch, sodass der Ausgang auf Low gezogen wird. Bei Low-Eingang sperrt der Transistor, der Ausgang wird über den Pull-Up-Widerstand high.

AND-Gatter

Kombiniert mehrere Transistoren in Serie: Nur wenn alle Eingänge high sind, können alle Transistoren leiten und der Ausgang wird low (bei NAND) oder high, bei AND mit nachgeschaltetem Inverter.

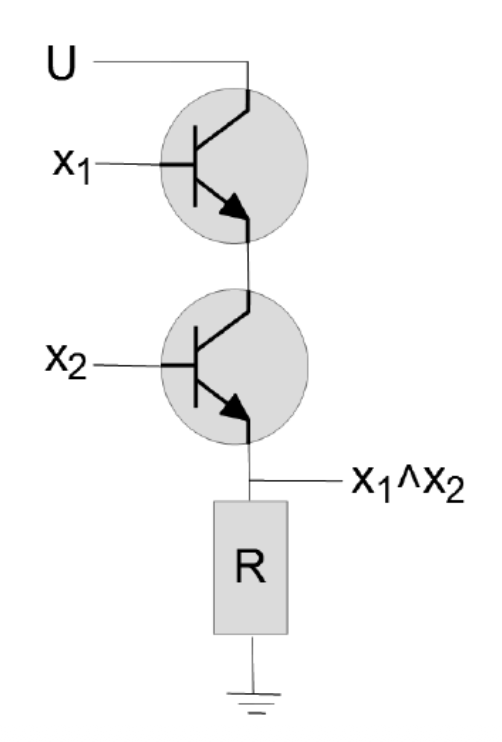
OR-Gatter

Transistoren parallel geschaltet: Ein einziger high-Eingang reicht aus, um den Ausgangszustand zu ändern. Die ODER-Funktion wird oft durch NOR mit nachgeschaltetem Inverter realisiert.

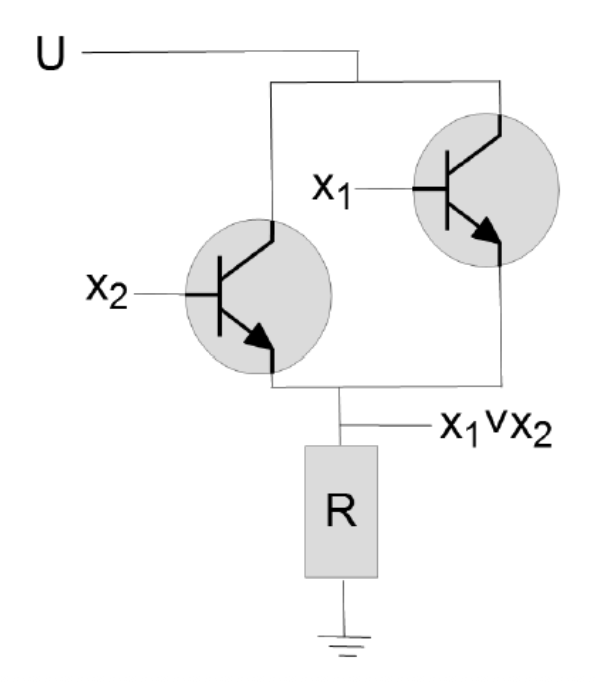
Schaltsymbole

Inzwischen hat sich (bei uns) die IEC (International Electronical Commission) Norm durchgesetzt. Die Schaltsymbole sehen wie folgt aus:

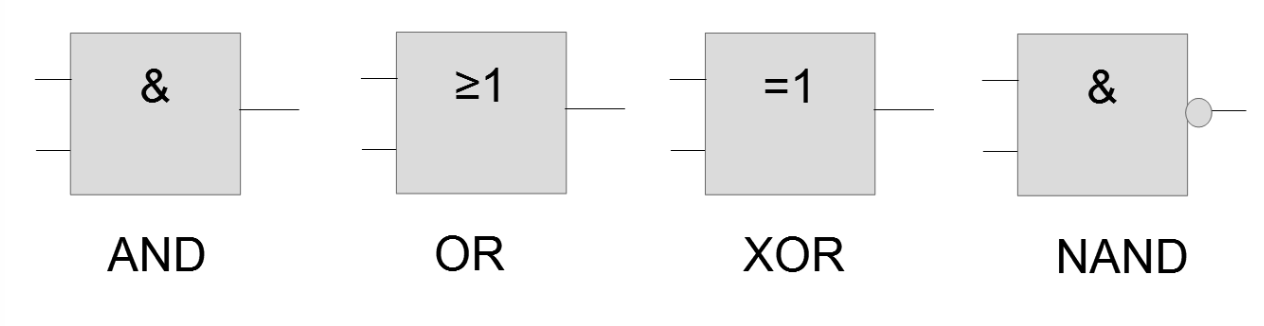
Dekodierer

Wandelt einen binären Code in eine Aktivierung einer bestimmten Ausgangsleitung um. Ein n-zu-$2^n$-Dekodierer hat $n$ Eingänge und $2^n$ Ausgänge. Anwendungen: Speicher-Adressdecodierung, 7-Segment-Ansteuerung, Steuerlogik.

Multiplexer, MUX

Wählt eines von mehreren Eingangssignalen basierend auf einem Steuercode aus. Funktionell ein schaltbarer Weichensteller. Ein 2:1-MUX realisiert: \( Y = (\overline{S} \cdot D_0) + (S \cdot D_1) \). Anwendungen: Datenauswahl, parallele-zu-seriell-Wandlung, Logikimplementierung.

Komparator

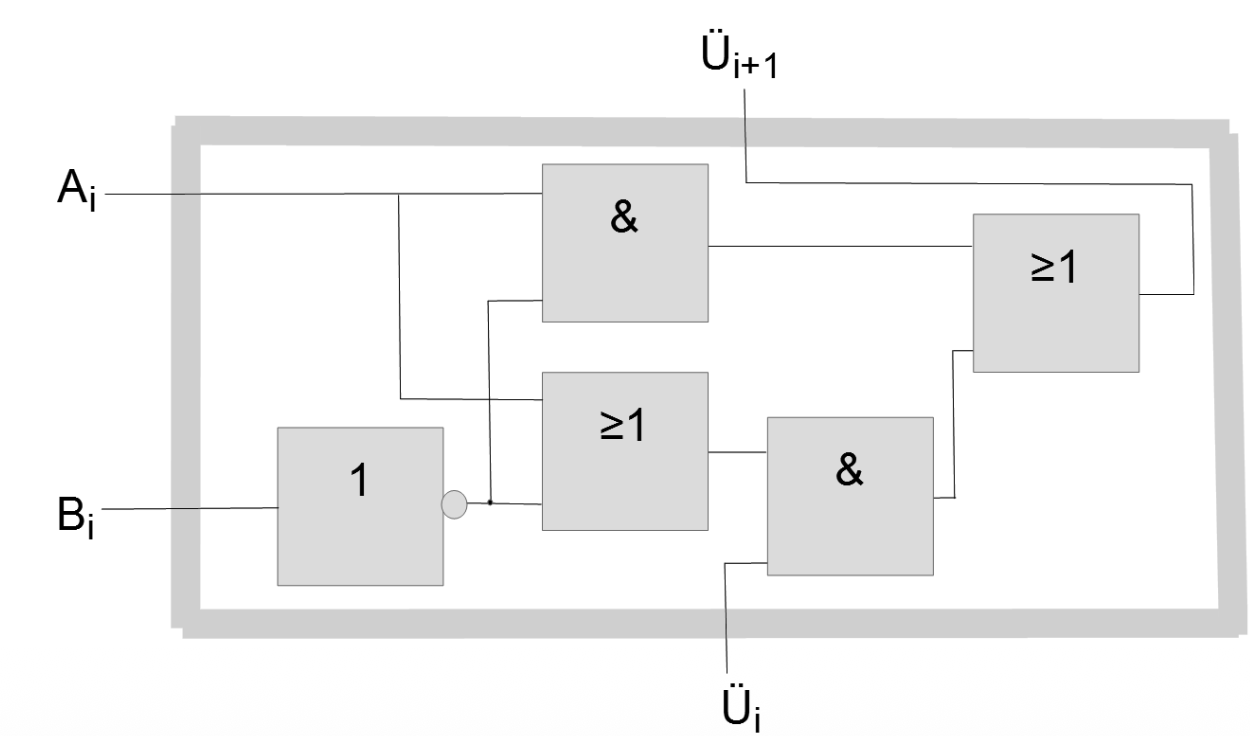
Vergleicht zwei Binärzahlen bitweise unter Berücksichtigung von Übertragsinformation. Der mehrstufige Aufbau ermöglicht den Vergleich beliebig langer Zahlen. Die Übertragsfunktion lautet:

\[ U_{i+1} = A_i \cdot \overline{B_i} + U_i \cdot (A_i + \overline{B_i}) \]

Diese Logik entscheidet, ob bis zur aktuellen Stelle $A$ größer als $B$ ist.

Addierwerke

Es gibt zwei Addierwerke:

• Halbaddierer

  Addiert zwei Bits ohne Übertragseingang: Summe = \( A \oplus B \), Übertrag = \( A \cdot B \)

  

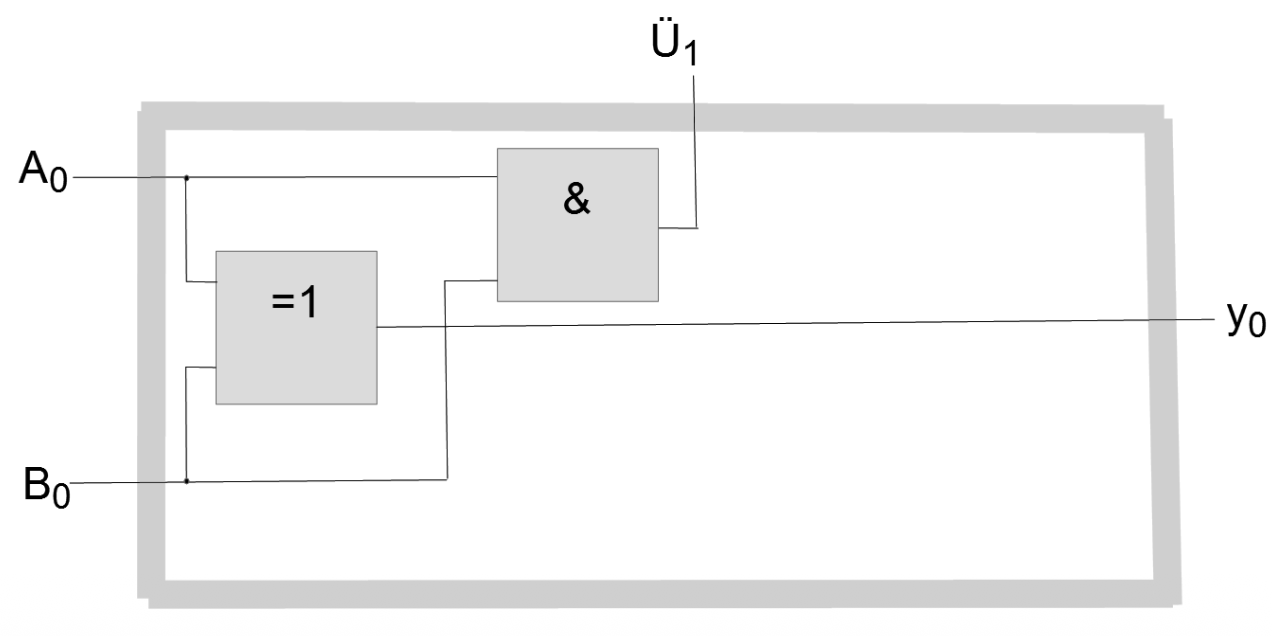
• Volladdierer

  Addiert zwei Bits mit Übertragseingang: Summe = \( A \oplus B \oplus C_{in} \), Übertrag = \( A \cdot B + C_{in} \cdot (A \oplus B) \)

  

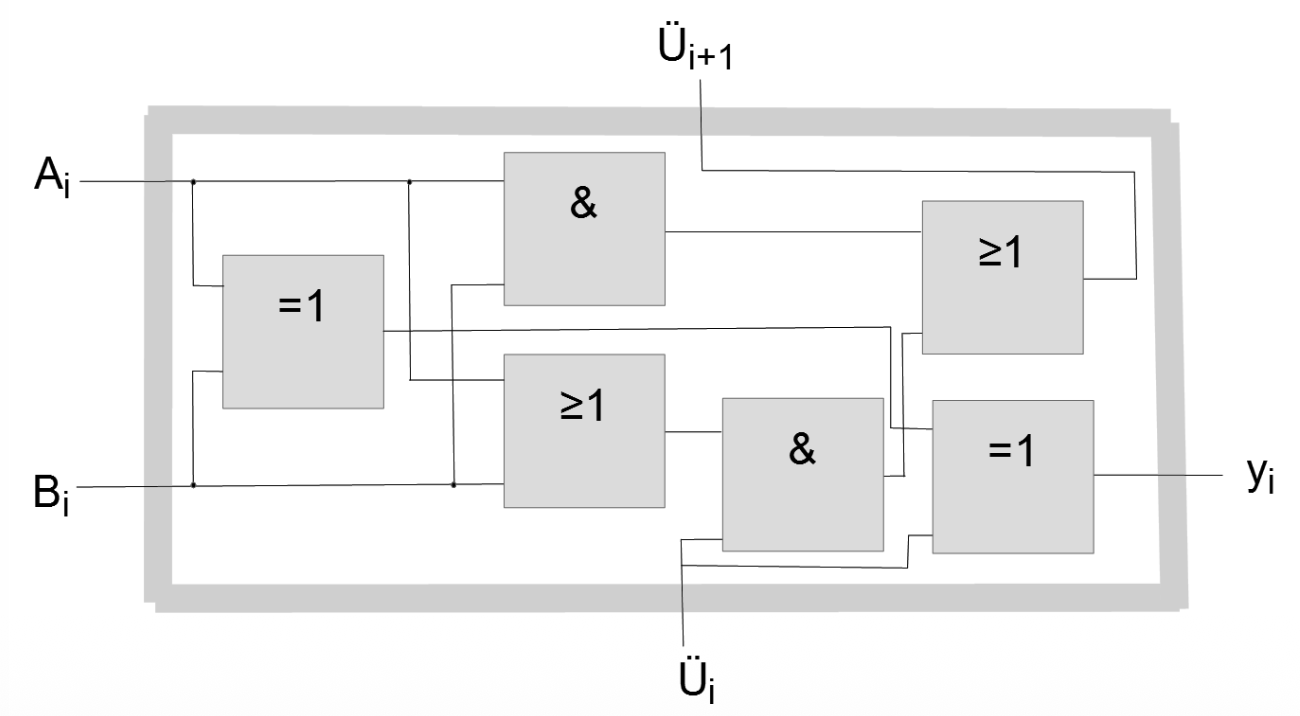
Bemerkung

Durch kaskadierte Volladdierer entstehen $n$-Bit-Addierwerke für arithmetische Operationen in Prozessoren.

Race Conditions

Durch unterschiedliche Signallaufzeiten in verschiedenen Pfaden einer Schaltung können kurzzeitige Fehlzustände, Glitches genannt, auftreten. Diese Race Conditions entstehen, wenn Signale asynchron durch die Logik propagieren.

Gegenmaßnahmen Race Conditions

Um Race Conditions zu vermeiden können folgende Gegenmaßnahmen unternommen werden:

• Synchronisation durch Taktung

• Hazard-Abdeckung in booleschen Funktionen

• Pipelinierung kritischer Pfade

• Verwendung von synchronen Schaltwerken