RLC - Parallelschaltung

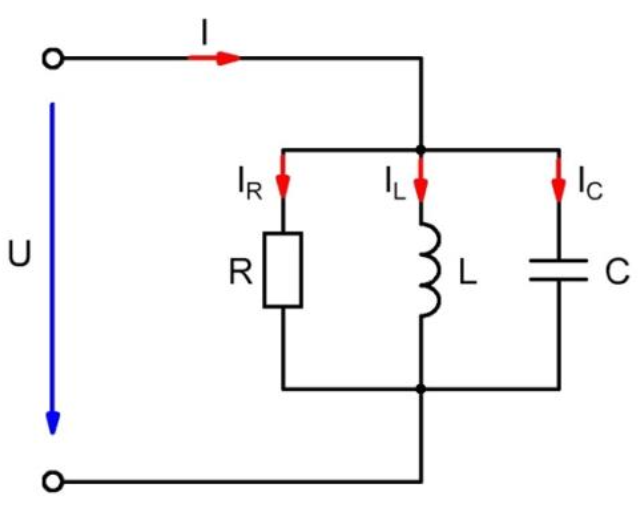
Schaltung

RLC Reihenschaltung

  1. Bei einer RLC-Reihenschaltung wird die Spannung \( I \) als Bezugsgröβe gewählt.

  2. Der Strom \( I_R \) liegt mit der Spannung \( U \) in Phase.

  3. Der Strom \( I_L \) eilt dem Strom \( I \) um 90\( ^\circ \) nach.

  4. Der Strom \( I_C \) eilt dem Strom \( I \) um 90\( ^\circ \) voraus.

  5. Die Phasenverschiebung zwischen \( I_C \) und \( I_L \) beträgt 180\( ^\circ \), das heiβt, die beiden Spannungen sind entgegengesetzt gerichtet.

Strom

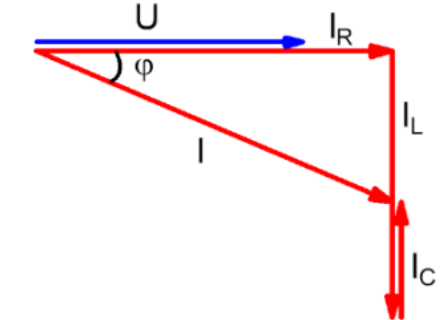RLC Spannungsdreieck $$ I = \sqrt{I_R^2 + (I_L - I_C)^2} $$ $$ \sin(\varphi) = \frac{I_L - I_C}{I} $$ $$ \cos(\varphi) = \frac{I_R}{I} $$ $$ \tan(\varphi) = \frac{I_L - I_C}{I_R} $$

Leitwert

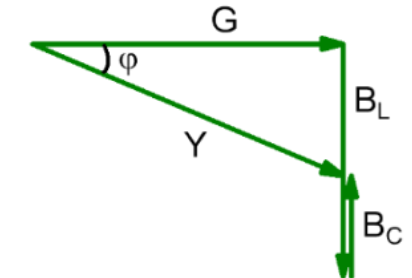RLC Widerstandsdreieck $$ Y = \sqrt{G^2 + (B_L - B_C)^2} $$ $$ \sin(\varphi) = \frac{B_L - B_C}{Y} $$ $$ \cos(\varphi) = \frac{G}{Y} $$ $$ \tan(\varphi) = \frac{B_L - B_C}{G} $$

Leistung

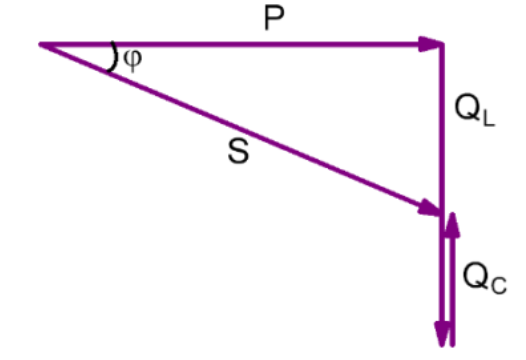RLC Leistungsdreieck $$ S = \sqrt{P^2 + (Q_L - Q_C)^2} $$ $$ \sin(\varphi) = \frac{Q_L - Q_C}{S} $$ $$ \cos(\varphi) = \frac{P}{S} $$ $$ \tan(\varphi) = \frac{Q_L - Q_C}{P} $$