RL - Parallelschaltung

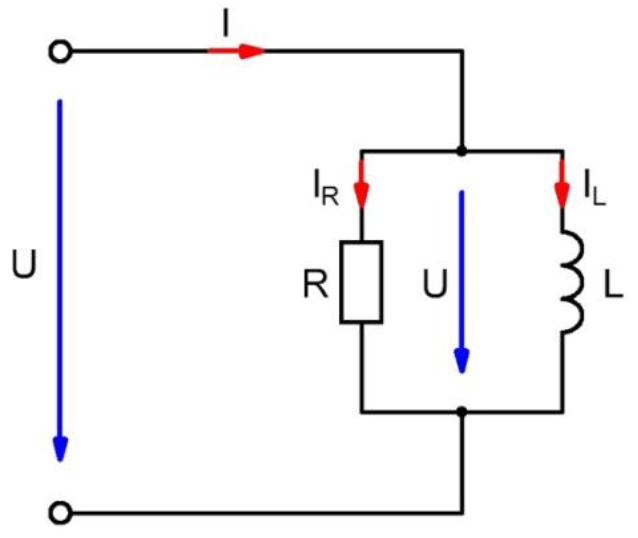
Schaltung

RL Parallelschaltung

  1. Am Wirkwiderstand \( R \) und an der Induktivität \( L \) liegt die gleiche Spannung \( U \). an.

  2. Durch \( R \) fließt der Strom \( I_R \). Er liegt mit \( U \) in Phase.

  3. Durch \( X_L \) fließt der Strom \( I_L \). Er eilt \( U \) um 90\( ^\circ \) nach.

  4. Deshalb müssen auch die Ströme \( I_R \) und \( I_L \) um 90\( ^\circ \) phasenverschoben sein.

Stromverhalten, Spannungsverhalten

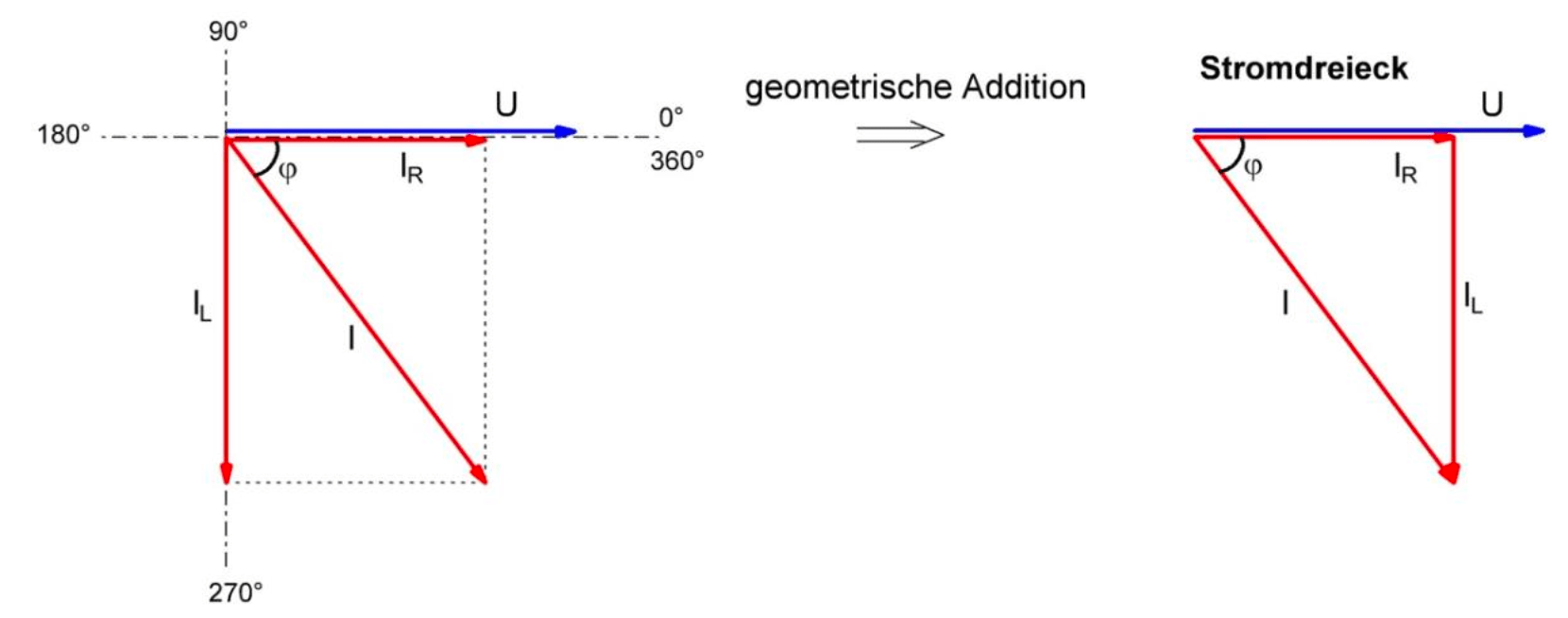$$ I^{2}=I^{2}_{R}+I^{2}_{L} $$ $$ \Leftrightarrow I^2 = \sqrt{I^{2}_{R}+I^{2}_{L}}$$ $$ \sin(\varphi) = \frac{I_L}{I}$$ $$ \cos(\varphi) = \frac{I_R}{I}$$ $$ \tan(\varphi) = \frac{I_L}{I_R}$$

Leitwertverhalten

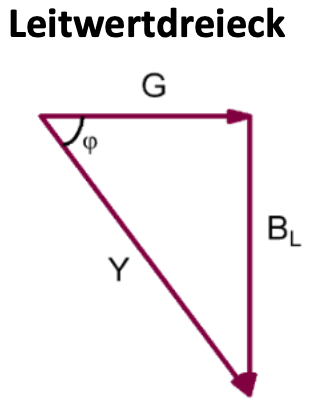
Leitwertdreieck

Bestimmung über Ohmsches Gesetz

$$ G=\frac{I_{R}}{U} =\frac{1}{R} $$ $$B_{L}=\frac{I_{L}}{U} =\frac{1}{X_{L}} $$ $$Y=\frac{1}{U} =\frac{1}{Z} $$

Bestimmung über geometrische Addition

$$Y^{2}=G^{2}+B^{2}_{L}$$ $$\Leftrightarrow Y = \sqrt{G^{2}+B^{2}_{L}} $$ $$ \sin(\varphi) = \frac{G}{Y}$$ $$ \cos(\varphi) = \frac{B_L}{Y}$$ $$ \tan(\varphi) = \frac{B_L}{G}$$

Leistungsverhalten

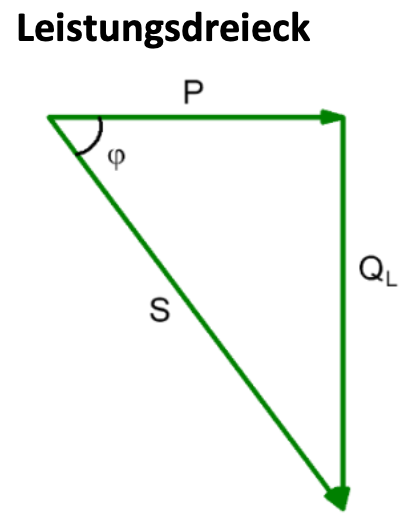Leistungsdreieck $$ P = U \cdot I_R $$ $$ Q_L = U \cdot I_L $$ $$ S = U \cdot I $$ $$ S^{2}=P^{2}+Q^{2}_{L}$$ $$ \Leftrightarrow S = \sqrt{P^{2}+Q^{2}_{L}} $$ $$ \sin(\varphi) = \frac{P}{S}$$ $$ \cos(\varphi) = \frac{Q_L}{S}$$ $$ \tan(\varphi) = \frac{Q_L}{P}$$